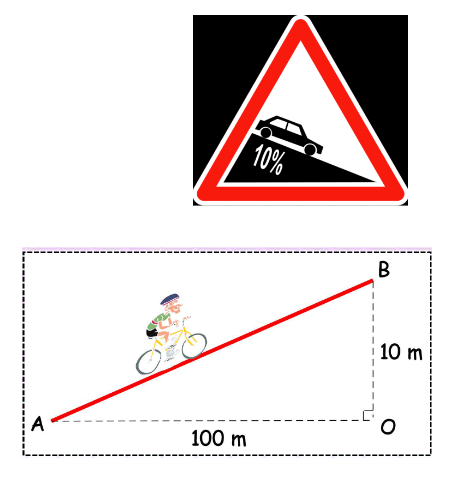
Pente d'une droite dans un repère orthonormé

• Dans ( O;I,J) un repère orthonormé du plan.
  
  
  
  
  
• Toute droite est plus ou moins "inclinée" par rapport à l'axe horizontal  (Ox) des abscisses.
  
  
• Comment mesurer l'inclinaison d'une droite dans un repère ?
  
  
  • À chaque inclinaison (non verticale, non parallèle à l'axe des ordonnées (Oy))
    corresponds un et un seul nombre réel \(a  \in  \mathbb R \)
    qui mesure l'inclinaison de la droite ( et réciproquement )
    
    Ce nombre est appelé "la pente" ou "le coefficient directeur" de la droite.
    
    Pour calculer ce nombre :
    
    
    • Il suffit de connaître les coordonnées de deux points de la droite \(A(x_A;y_A) \)  et \(B(x_B;y_B) \)
      et d'appliquer la formule suivante : \(  \boxed{  \color{white} {a = \dfrac{y_B-y_A}{x_B-x_A} } }\)
      
      
  • Si la droite est "verticale", on dit qu'elle a une pente infinie.
    
    
    
    
  • Sur les panneaux de sécurité routière, la pente est exprimée en pourcentage
    et n'indique pas de signe (positif ou négatif)