Une droite
( sans limite, ni à gauche , ni à droite)
sur laquelle on souhaite placer tous les "nombres réels "

choisis un point \(O\) auquel on associe le nombre \(0\)
choisis un point \(I\) auquel on associe le nombre \(1\)
et après ???

Les nombres Entiers Naturels : \( \mathbb N \)
Régulièrement espacés sur la droite,
Le premier est 0, son successeur (à droite par convention ) est 1, ainsi de suite ... (espacés d'une unité)
Il n'y a pas de plus grand entier naturel !

Les nombres Entiers Relatifs : \( \mathbb Z \)
Régulièrement espacés sur la droite,
0 "au centre"
1 son successeur à sa droite et ainsi de suite ... (espacés d' une unité)
-1 son prédécesseur à sa gauche et ainsi de suite ... (espacés d' une unité)
Il n'y a ni plus grand ni plus petit entier relatif !
On a ainsi tous les entiers naturels ainsi que l'opposé de chacun .

Peut-on placer d'autres nombres sur cette droite ?
Si oui,
Où ?

Entre 0 et 1 ?

Des nombres Décimaux : \( \mathbb D \)
Espacés régulièrement de \( 0,1 = \dfrac{1}{10} = 10^{-1}\) en \( 0,1 \)
Peut-on en ajouter d'autres ?
Par exemple entre 0,3 et 0,4 ?

Des nombres décimaux : \( \mathbb D \)
Espacés régulièrement de \( 0,01 = \dfrac{1}{100} = \dfrac{1}{10^2} = 10^{-2} \) en \( 0,01 \)
Peut-on en ajouter d'autres ?
Par exemple entre 0,33 et 0,34 ?

Des nombres décimaux : \( \mathbb D \)
Espacés régulièrement de \( 0,001 = \dfrac{1}{1000} = \dfrac{1}{10^3} = 10^{-3}\) en \( 0,001 \)
Peut-on en ajouter d'autres ?
Par exemple entre 0,333 et 0,334 ?

Des nombres décimaux : \( \mathbb D \)
Espacés régulièrement de \( 0,0001 = \dfrac{1}{10000} = \dfrac{1}{10^4} = 10^{-4}\) en \( 0,0001 \)
et ensuite ?

Des nombres décimaux : \( \mathbb D \)
Espacés régulièrement de \( 0,00001 = \dfrac{1}{100000} = \dfrac{1}{10^5} = 10^{-5}\) en \( 0,00001 \)
et ensuite ?

Des nombres décimaux : \( \mathbb D \)
Espacés régulièrement de \( 0,000001 = \dfrac{1}{1000000} = \dfrac{1}{10^6} = 10^{-6}\) en \( 0,000001 \)
et ensuite ?

Avec l'ensemble des nombres Décimaux
qui sécrivent sous la forme fractionnaire : \( \boxed{ d = \dfrac{z}{10^n} } \)
avec \( n \) entier naturel ( \( n \in \mathbb N \) ) et \( z \) entier relatif ( \( z \in \mathbb Z \) )

ou encore sous la forme décimale : \(d = z,s\) avec \( z \) entier relatif et \( s \) une suite infinie de chiffres

(à partir d'un certain rang, la partie décimale "n'a plus que des \(0\)" ou "que des \(9\)" )
(à partir d'un certain rang, la partie décimale est "périodique de période \(0\) ou \(9\)" ( -> voir ) )

Peut-on ainsi "remplir" toute la droite ?

C'est à dire : ASSOCIER à TOUT point de la droite un nombre décimal ?
Si non !
Donner un nombre NON DÉCIMAL !

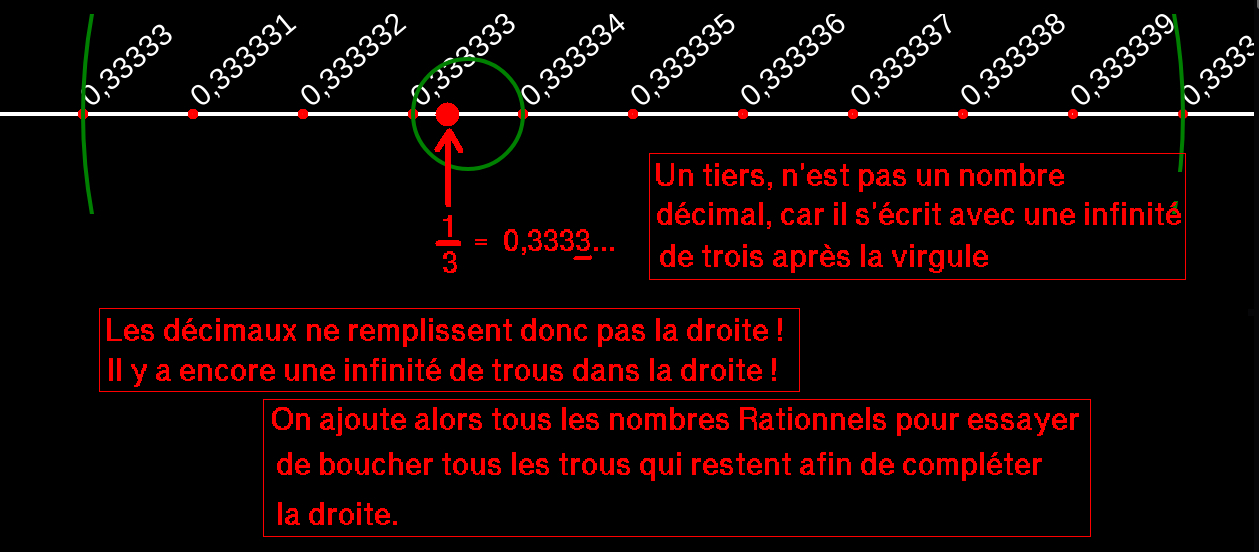
Les nombres suivants ne sont pas décimaux
(admis pour le moment)
Ce sont des nombres RATIONNELS : \( \mathbb Q \)
(ration, part,..)

De la forme \( \boxed{ \dfrac{z}{n} } \) avec \( n \) entier naturel non nul ( \( n \in \mathbb N^* \) ) et \( z \) entier relatif ( \( z \in \mathbb Z \))

(Voir -> l'Écriture décimale d'un rationnel ( ceci) et ( ceci) )

\( \dfrac{1}{3} ~~~\dfrac{2}{3}\)

\( \dfrac{1}{6} ~~~\dfrac{5}{6} \)

\( \dfrac{1}{7} ~~~\dfrac{2}{7} ~~~\dfrac{3}{7} ~~~\dfrac{4}{7} ~~~\dfrac{5}{7} ~~~\dfrac{6}{7} \)

\( \dfrac{1}{9} ~~~\dfrac{2}{9} ~~~\dfrac{4}{9} ~~~\dfrac{5}{9} ~~~\dfrac{7}{9} ~~~\dfrac{8}{9} \)

\( \dfrac{1}{11} ~~~\dfrac{2}{11} ~~~\dfrac{3}{11} ~~~\dfrac{4}{11} ~~~\dfrac{5}{11} ~~~\dfrac{6}{11} ~~~\dfrac{7}{11} ~~~\dfrac{8}{11} ~~~\dfrac{9}{11} ~~~\dfrac{10}{11} \)

\( \dfrac{1 }{12} ~~~ \dfrac{5 }{12} ~~~ \dfrac{7 }{12} ~~~ \dfrac{11 }{12} ~~~ \)

\( \dfrac{1 }{13} ~~~ \dfrac{2 }{13} ~~~ \dfrac{3 }{13} ~~~ \dfrac{4 }{13} ~~~ \dfrac{5 }{13} ~~~ \dfrac{6 }{13} ~~~ \dfrac{7 }{13} ~~~ \dfrac{8 }{13} ~~~ \dfrac{9 }{13} ~~~ \dfrac{10 }{13} ~~~ \dfrac{11 }{13} ~~~ \dfrac{12 }{13} ~~~ \)

\( \dfrac{1 }{14} ~~~ \dfrac{3 }{14} ~~~ \dfrac{5 }{14} ~~~ \dfrac{9 }{14} ~~~ \dfrac{11 }{14} ~~~ \dfrac{13 }{14} ~~~ \)

\( \dfrac{1 }{15} ~~~ \dfrac{2 }{15} ~~~ \dfrac{4 }{15} ~~~ \dfrac{7 }{15} ~~~ \dfrac{8 }{15} ~~~ \dfrac{11 }{15} ~~~ \dfrac{13 }{15} ~~~ \dfrac{14 }{15} ~~~ \)

\( \dfrac{1 }{17} ~~~ \dfrac{2 }{17} ~~~ \dfrac{3 }{17} ~~~ \dfrac{4 }{17} ~~~ \dfrac{5 }{17} ~~~ \dfrac{6 }{17} ~~~ \dfrac{7 }{17} ~~~ \dfrac{8 }{17} ~~~ \dfrac{9 }{17} ~~~ \dfrac{10 }{17} ~~~ \dfrac{11 }{17} ~~~ \dfrac{12 }{17} ~~~ \dfrac{13 }{17} ~~~ \dfrac{14 }{17} ~~~ \dfrac{15 }{17} ~~~ \dfrac{16 }{17} ~~~ \)

\( \dfrac{1 }{18} ~~~ \dfrac{3 }{18} ~~~ \dfrac{5 }{18} ~~~ \dfrac{7 }{18} ~~~ \dfrac{11 }{18} ~~~ \dfrac{13 }{18} ~~~ \dfrac{15 }{18} ~~~ \dfrac{17 }{18} ~~~ \)

\( \dfrac{1 }{19} ~~~ \dfrac{2 }{19} ~~~ \dfrac{3 }{19} ~~~ \dfrac{4 }{19} ~~~ \dfrac{5 }{19} ~~~ \dfrac{6 }{19} ~~~ \dfrac{7 }{19} ~~~ \dfrac{8 }{19} ~~~ \dfrac{9 }{19} ~~~ \dfrac{10 }{19} ~~~ \dfrac{11 }{19} ~~~ \dfrac{12 }{19} ~~~ \dfrac{13 }{19} ~~~ \dfrac{14 }{19} ~~~ \dfrac{15 }{19} ~~~ \dfrac{16 }{19} ~~~ \dfrac{17 }{19} ~~~ \dfrac{18 }{19} ~~~ \)



\( \dfrac{1 }{21} ~~~ \dfrac{2 }{21} ~~~ \dfrac{3 }{21} ~~~ \dfrac{4 }{21} ~~~ \dfrac{5 }{21} ~~~ \dfrac{6 }{21} ~~~ \dfrac{7 }{21} ~~~ \dfrac{8 }{21} ~~~ \dfrac{9 }{21} ~~~ \dfrac{10 }{21} ~~~ \dfrac{11 }{21} ~~~ \dfrac{12 }{21} ~~~ \dfrac{13 }{21} ~~~ \dfrac{14 }{21} ~~~ \dfrac{15 }{21} ~~~ \dfrac{16 }{21} ~~~ \dfrac{17 }{21} ~~~ \dfrac{18 }{21} ~~~ \dfrac{19 }{21} ~~~ \dfrac{20 }{21} ~~~ \)

\( \dfrac{1 }{22} ~~~ \dfrac{3 }{22} ~~~ \dfrac{5 }{22} ~~~ \dfrac{7 }{22} ~~~ \dfrac{9 }{22} ~~~ \dfrac{11 }{22} ~~~ \dfrac{13 }{22} ~~~ \dfrac{15 }{22} ~~~ \dfrac{17 }{22} ~~~ \dfrac{19 }{22} ~~~ \dfrac{21 }{22} ~~~ \)

\( \dfrac{1 }{23} ~~~ \dfrac{2 }{23} ~~~ \dfrac{3 }{23} ~~~ \dfrac{4 }{23} ~~~ \dfrac{5 }{23} ~~~ \dfrac{6 }{23} ~~~ \dfrac{7 }{23} ~~~ \dfrac{8 }{23} ~~~ \dfrac{9 }{23} ~~~ \dfrac{10 }{23} ~~~ \dfrac{11 }{23} ~~~ \dfrac{12 }{23} ~~~ \dfrac{13 }{23} ~~~ \dfrac{14 }{23} ~~~ \dfrac{15 }{23} ~~~ \dfrac{16 }{23} ~~~ \dfrac{17 }{23} ~~~ \dfrac{18 }{23} ~~~ \dfrac{19 }{23} ~~~ \dfrac{20 }{23} ~~~ \dfrac{21 }{23} ~~~ \dfrac{22 }{23} ~~~ \)

et ensuite ... ???

Une fois "ajoutés" tous les RATIONNELS sur la droite, a t-on "remplie" la droite ?
Sinon, donner un nombre non Rationnel !

L'ensemble des nombres Rationnels \( \mathbb Q \) contient tous,
et uniquement les nombres fractionnaires de la forme :
\( q = \displaystyle \frac{z}{n} \)
où \( n \) est un entier naturel non nul et \( z \) un entier relatif

ou encore sous la forme décimale :
\(q = z,n\underline{s}\)
où \( z \) un entier relatif, \( n \) est entier naturel et \( s \) est une suite infinie périodique de chiffres entre \( 0 \) et \(9\)

Mais !!! Par exemple, les nombres suivants ne sont pas rationnels, ils sont IRRATIONNELS

(admis pour le moment)

(-> Voir l'Écriture décimale d'un irrationnel ( ceci) et ( ceci) )

\( \pi \)

\( \sqrt{2} \)

\( \sqrt{3} \)

\( \sqrt{5} \)

\( \sqrt{6} \)

\( \sqrt{7} \)

\( \sqrt{8} \)

\( \sqrt{10} \)

\( \sqrt{11} \)

\( \sqrt{12} \)

\( \sqrt{13} \)

\( \sqrt{14} \)

\( \sqrt{15} \)

\( \sqrt{17} \)

\( ... \)

Et on définit les nombres IRRATIONNELS comme l'ensemble des nombres qui ne sont pas rationnels

Un nombre est Irrationnel si et seulement si :
l'écriture décimale de ce nombre a une partie décimale qui n'est pas "périodique à partir d'un certain rang"

Il suffit d'ajouter aux précedents ( les Rationnels ) les nombre Irrationnels
pour COMPLÉTER la droite numérique des NOMBRE RÉELS : \( \mathbb R \)

On a ainsi ASSOCIÉ à chaque point de la droite un et un seul nombre RÉEL


Il n'y a plus de place pour "intercaler" d'autres nombres !

C'est Complet !