• Qu'ont de particulier les suites de nombres suivantes  ?
  
  
  (✓ Remarque) (✗ Fermer Remarque )
  
  La valeur du terme suivant est fonction de la valeur du terme qui le précède.
  Une seule opération pour passer d'un terme à l'autre.
  La suite est définie par une formule de récurrence de la forme \( u_{n+1} = f(u_n) \) où \(f\) est une formule à trouver
  (✓ Réponse ) (✗ Fermer Réponse )
  
  Pour chacune des suites de nombres précédentes,
  
  Pour passer d'un terme à l'autre , on multiplie toujours par un même nombre.
  Les suites précédentes sont dites "géométriques".
  Le nombre par lequel on multipie pour passer d'un terme à l'autre est appelé la "raison" de la suite et est noté \(q\).





---



• Déterminer les termes suivants :
  
  
  • \( \huge {V_0 = 100 } \)
    
    
  • \( \huge {V_1 = 200} \)
    
    
  • \( \huge {V_2 = 400 } \)
    
    
  • \( \huge {V_3 = ? } \)
    
    
  • \( \huge {V_4 = ? } \)
    
    
  • \( \huge {V_{10} = ? } \)
    
    
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  
  Suite récurrente simple
  
  Suite géométrique
  
  À partir du deuxième terme, on trouve la valeur du terme en multipliant par 2 le terme précédent.
  
  \( \huge {V_{n+1} = V_{n} \times 2 } \)
  
  \( \huge {V_3 = V_2 \times 2 = 400 \times 2 = 800} \)
  
  \( \huge {V_4 = 800 \times 2 = 1600} \)
  
  
  \( \huge {V_{10} =   100 \times 2^{10} = 102400} \)       (calculatrice)



---



• Déterminer les termes suivants :
  
  
  • \( \huge {u_1 = 2 } \)
    
    
  • \( \huge {u_2 = 6} \)
    
    
  • \( \huge {u_3 = 18 } \)
    
    
  • \( \huge {u_4 = ? } \)
    
    
  • \( \huge {u_5 = ? } \)
    
    
  • \( \huge {u_{10} = ? } \)
    
    
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  
  Suite récurrente simple
  
  Suite géométrique
  
  À partir du deuxième terme, on trouve la valeur du terme en multipliant par 3 le terme précédent.
  
  \( \huge {u_{n+1} = u_{n} \times 3 } \)
  
  \( \huge {u_4 = u_3 \times 3 } \)
  
  \( \huge {u_4 = 18 \times 3 = 54} \)
  
  \( \huge {u_5 = 54 \times 3 = 162} \)
  
  \( \huge {u_{10} =   2 \times 3^{9} = 39366} \)       (calculatrice)



---



• Déterminer les termes suivants :
  
  
  • \( \huge {W_0 = 2048 } \)
    
    
  • \( \huge {W_1 = 1024} \)
    
    
  • \( \huge {W_2 = 512 } \)
    
    
  • \( \huge {W_3 = ? } \)
    
    
  • \( \huge {W_4 = ? } \)
    
    
  • \( \huge {W_{10} = ? } \)
    
    
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  
  Suite récurrente simple
  
  Suite géométrique
  
  À partir du deuxième terme, on trouve la valeur du terme en multipliant par 0,5 le terme précédent.
  
  \( \huge {W_{n+1} = W_{n} \times 0,5} \)
  
  \( \huge {W_3 = W_2 \times 0,5 = 512 \times 0,5 = 256} \)
  
  \( \huge {W_4 = 256 \times 0,5 = 128} \)
  
  
  \( \huge {W_{10} =   2048 \times 0,5^{10} = 2} \)       (calculatrice)



---



• Déterminer le terme suivant :
  
  
  
  
  
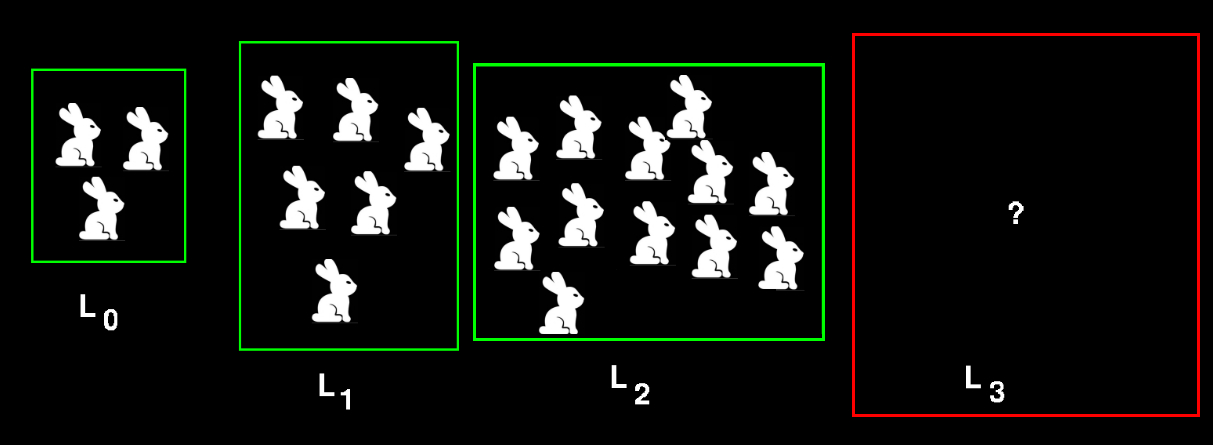
  • \( \huge {L_n = } \)  nombre de petits lapins à l'étape \(  \huge { n } \)
    
    
  • \( \huge {L_0 = ? } \)
    
    
  • \( \huge {L_1 = ?} \)
    
    
  • \( \huge {L_2 = ?} \)
    
    
  • \( \huge {L_3 = ? } \)
    
    
  • \( \huge {L_{10} = ? } \)
    
    
  • \( \huge {L_{100} = ? } \)
    
    
  • \( \huge {L_{n} = ? } \)
    
    
  • \( \huge {L_{n} = ? } \)
    
    
  • Trouver la plus petite valeur de \( \huge { n } \) pour laquelle \( \huge {L_{n} \leq 10 000 } \)
    
    
  • Formule de Récurrence :   \( \huge {L_{n+1} = ? } \)
    
    
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  



---



• Déterminer le terme suivant :
  
  
  
  
  
  • \( \huge {L_n = } \)  nombre de petits lapins à l'étape \(  \huge { n } \)
    
    
    
  • \( \huge {L_1 = ?} \)
    
    
  • \( \huge {L_2 = ?} \)
    
    
  • \( \huge {L_3 = ? } \)
    
    
  • \( \huge {L_4 = ? } \)
    
    
  • \( \huge {L_{10} = ? } \)
    
    
  • \( \huge {L_{100} = ? } \)
    
    
  • \( \huge {L_{n} = ? } \)
    
    
  • Trouver la plus petite valeur de \( \huge { n } \) pour laquelle \( \huge {L_{n} \leq 10 000 } \)
    
    
  • Formule de Récurrence :   \( \huge {L_{n+1} = ? } \)
    
    
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  



---



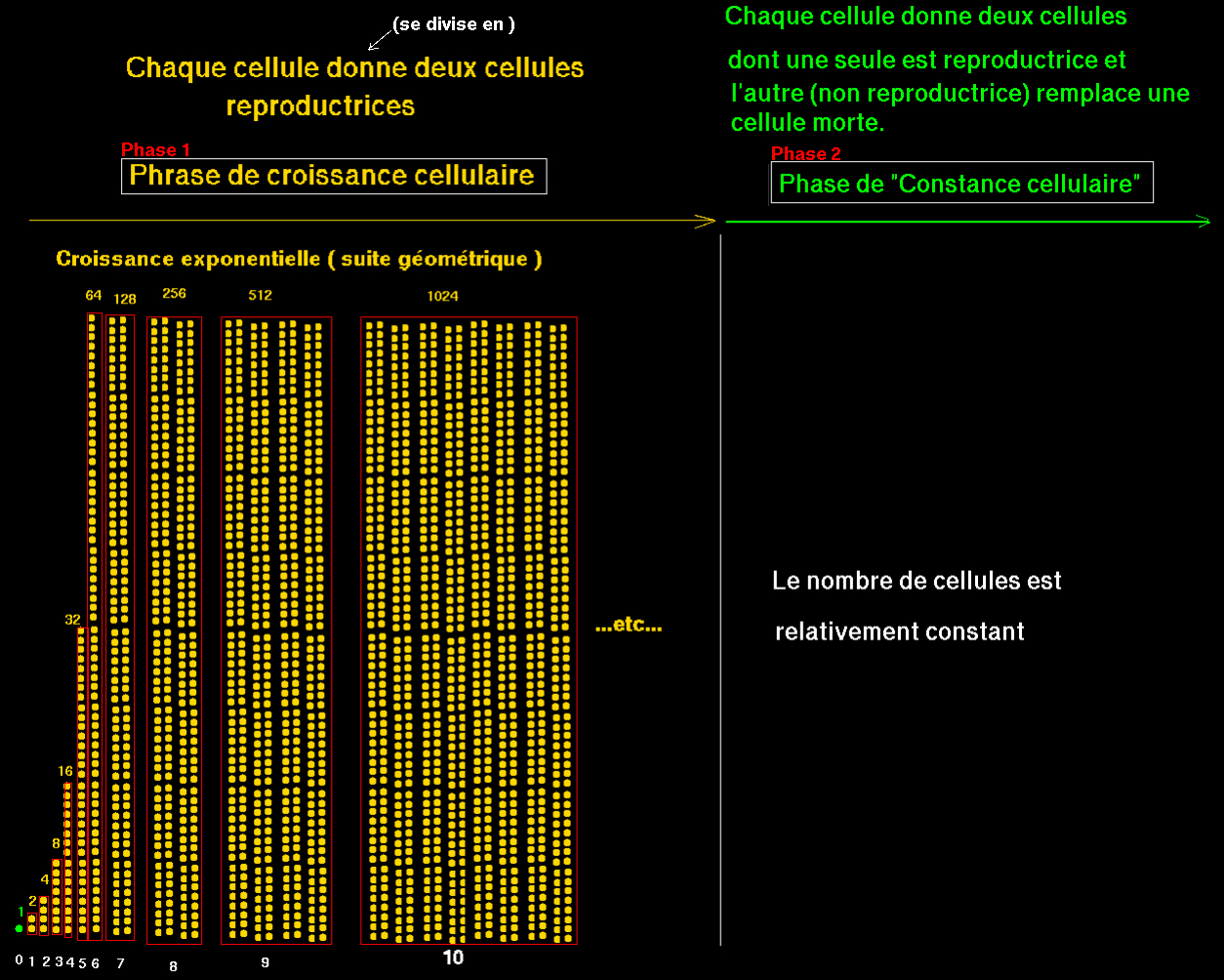
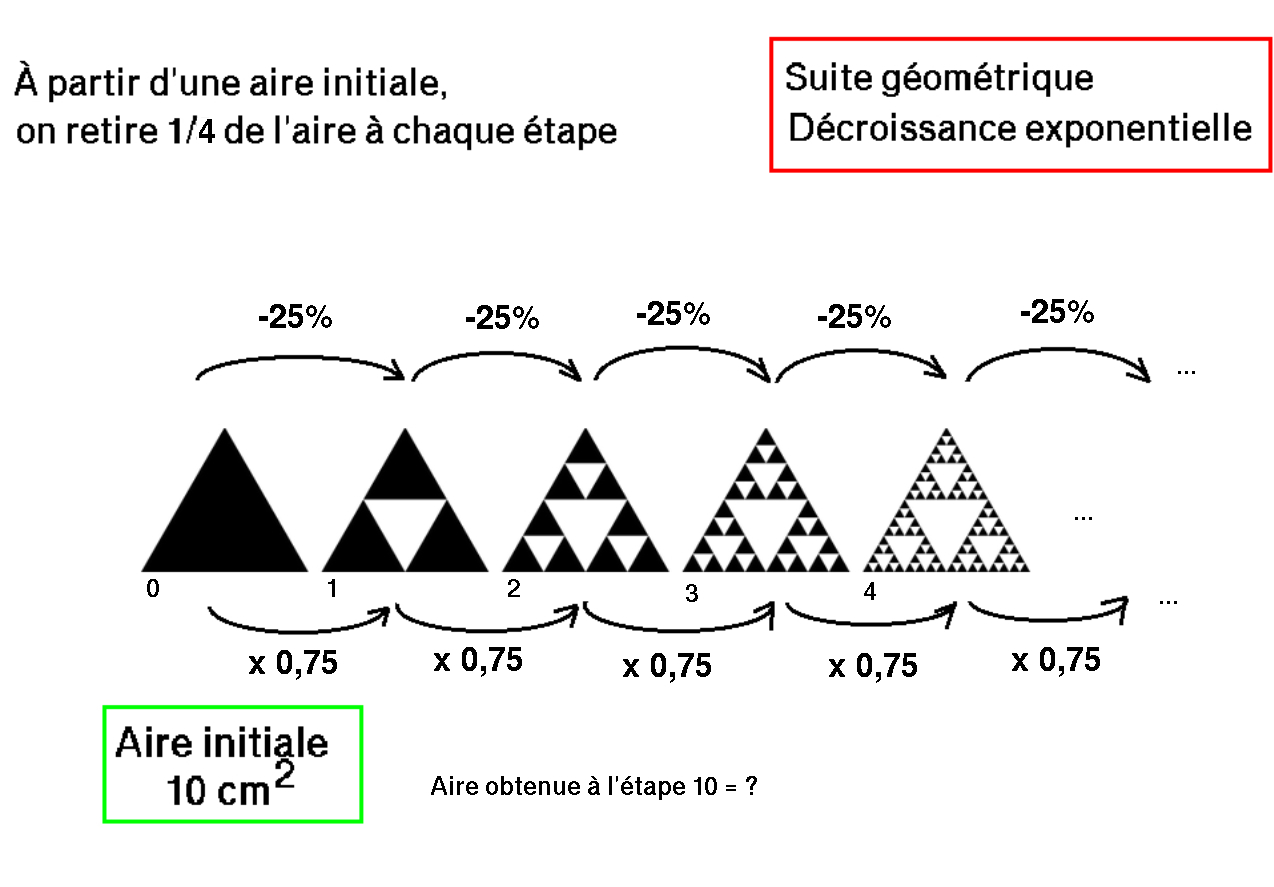
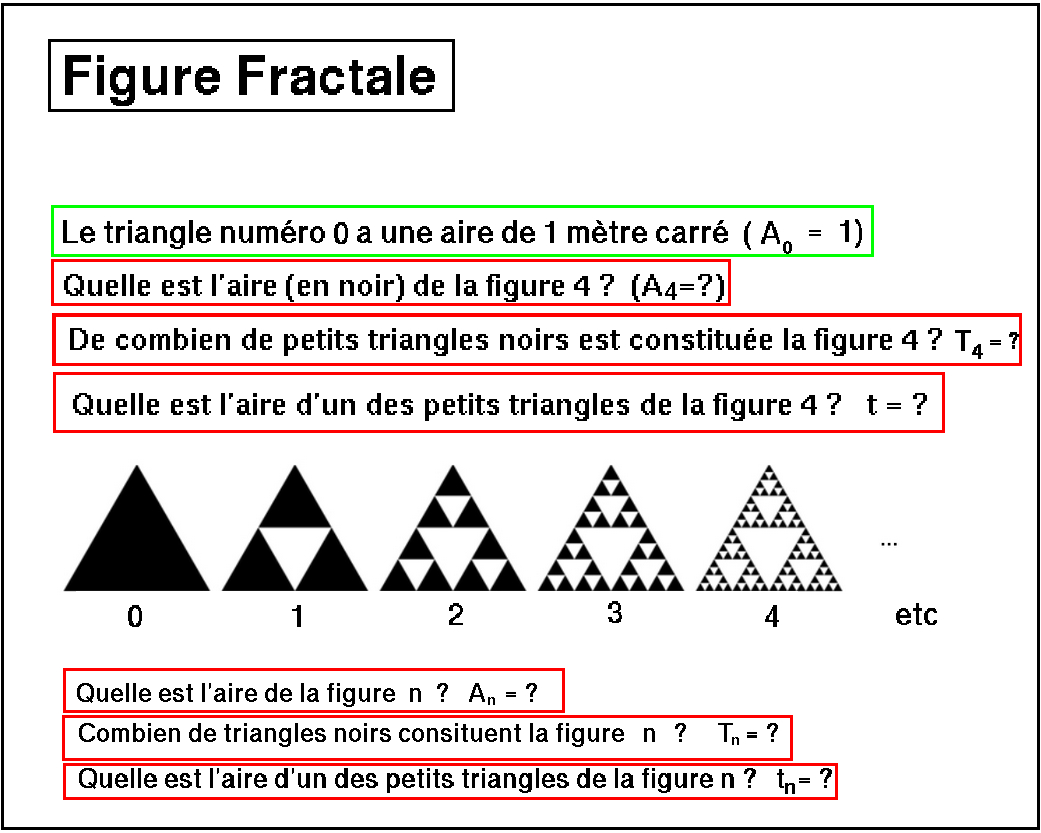
• Multiplication de cellules vivantes :
  
    



---



• Placement en banque à intérêts composés annuels :
  
    



---



• Figure Fractale :
  
    



---



• Figure Fractale :
  



---



• Flocon de Koch (html)
  
  

  ---

  
  
• Arbre Fractal (html)
  



---



• Flocon de Koch avec réduction (html)
  



---



• Nénuphar
  
  
  Un nénuphar double de surface chaque jour,
  Ce nénuphar recouvre exactement une mare 10 jours après avoir été mis en place.
  Après combien de jours recouvre t-il  exactement la moitié de la mare ?
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  
  9 jours



---



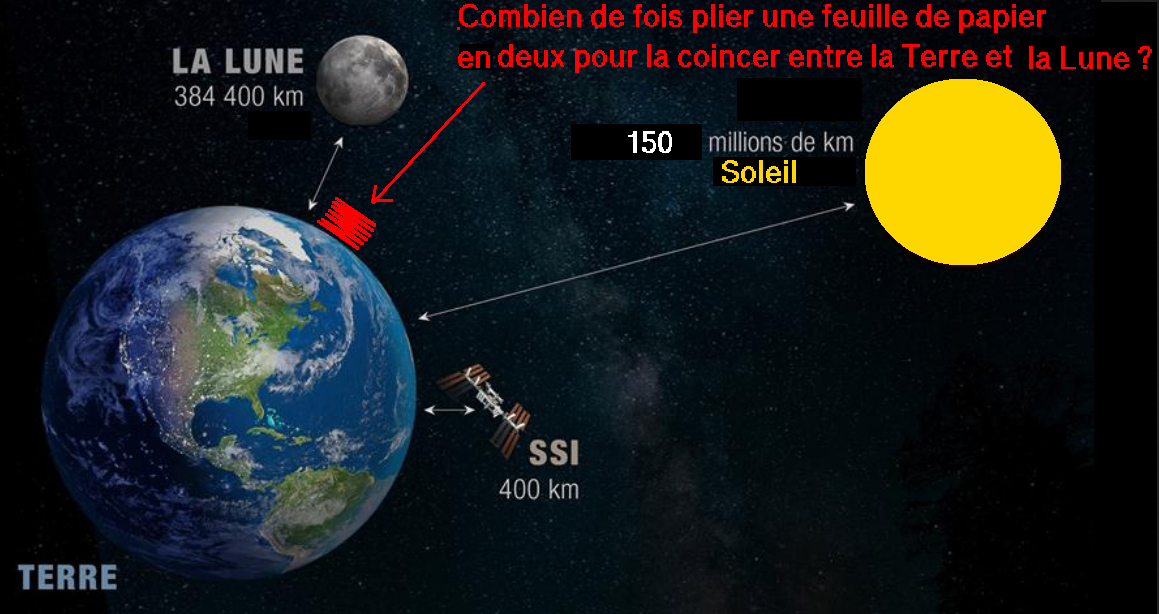
• Coincer une feuille de papier entre la terre et la lune ?
  
  
  Combien de fois suffit-il de plier une feuille de papier de 0,1 millimètres d'épaisseur en deux pour pouvoir la coincer entre la terre et la lune ? ( la feuille est aussi grande que besoin )
  
  
  
  
  (✓ Réponse ) (✗ Fermer Réponse )
  
  

  1. Entre la terre et l'ISS  ?  (400 km d'altitude)
     
     
     • Il suffit de résoudre l'équation suivante :
       
       \(0,1 \times 2^n = 400 \times 1000 \times 1000\)   (tout en millimètres)
       
       \(0,1 \times 2^n = 4 \times 10^{8}\)
       
       \( 2^n = \dfrac{4 \times 10^{8}}{10^{-1}}\)
       
       \( 2^n = 4 \times 10^{9}\)
       
       \( ln(2^n) =  ln(4 \times 10^{9})\)
       
       \(n \times ln(2) =  ln(4 \times 10^{9})\)
       
       \(n =  \dfrac{ln(4 \times 10^{9})}{ln(2)}\)
       
       \(n \simeq 31,9\)
       
       Il suffit de plier la feuille 31 fois.
       
       Vérification :  
       
       \(0,1 \times 2^{32} \simeq 429496729 \) millimètres
       
       \(0,1 \times 2^{32} \simeq 429 \) kilomètres
       
       
  
  
  
  2. Entre la terre et la Lune   ?  (384 400 km ) :
     
     \(0,1 \times 2^n = 384 400 \times 1000 \times 1000\)   (tout en millimètres)
     
     
     \(n =  \dfrac{ln(3844 \times 10^{8})}{ln(2)}\)
     
     \(n \simeq 38,4\)
     
     Il suffit de plier la feuille 39 fois.
     
     Vérification :  
     
     \(0,1 \times 2^{39} \simeq 54975581389 \) millimètres
     
     \(0,1 \times 2^{39} \simeq 549755 \) kilomètres
  
  
  
  3. Entre la terre et le Soleil   ?  (150 000 000 km ) :
     
     
     \(n =  \dfrac{ln(15 \times 10^{13})}{ln(2)}\)
     
     \(n \simeq 50,4\)
     
     Il suffit de plier la feuille 51 fois.
     
     Vérification :  
     
     \(0,1 \times 2^{51} \simeq 225179981368525 \) millimètres
     
     \(0,1 \times 2^{51} \simeq 225 000 000\) kilomètres