Image Mentale
de la
Droite Discrète
des
Nombres Entiers Relatifs \( \mathbb Z\)
- CONSTRUCTION de L'IMAGE MENTALE de la DROITE des ENTIERS RELATIFS
- DROITE DISCRÈTE des ENTIERS RELATIFS

- Une droite avec 0 pour point de départ.
- 1 à droite de 0 sur cette droite.
- 2 à droite de 1 sur cette demi-droite (avec le même écart qu'entre 0 et 1)
- et ainsi de suite vers la droite, jusqu'à l'infini...
- L'ensemble des nombres entiers relatifs contient tous les nombres entiers naturels.
- -1 à gauche de 0 sur cette demi-droite (avec le même écart qu'entre 0 et 1)
- -2 à gauche de -1 sur cette demi-droite (avec le même écart qu'entre 0 et 1)
- et ainsi de suite vers la gauche, jusqu'à l'infini...
- Les nombres entiers relatifs sont rangés sur la "droite discrète des entiers relatifs ".
- La droite discrète des nombres entiers relatifs est infinie vers la droite, (elle est "infiniment grande vers la droite) et infinie vers la gauche.
- Les entiers relatifs sont régulièrement espacés de 1 unité en partant de 0 vers la droite ou vers la gauche (il y a toujours une unité entre un entier relatif et son "successeur" et entre un entier relatif et son prédécesseur)
- On utilise le mot "discrète" car entre deux entiers relatifs successif, il n'y a aucun autre entier relatif strictement compris.
- À chaque nombre entier relatif il correspond un point de la droite discrète des nombres entiers relatifs.
- Il existe des points de la droite discrète des nombres entiers relatifs auxquels il ne correspond aucun nombre entier relatif.
- POSITIF, NÉGATIF, NUL

- Le nombre 0 (zéro) est la séparation entre les nombres entiers relatifs (au centre de l'image mentale, car une droite n'a pas de centre)
positifs stricts qui sont "à droite" → de 0,
et les nombres entiers relatifs
négatifs stricts qui sont "à gauche" ← de 0.
- Quand on dit " x est positif" en Français,
on sous-entend "x est positif ou nul" en Mathématiques et on note x \( \geqslant\) 0
- Quand on dit "négatif" en Français,
on sous-entend "négatif ou nul" en Mathématiques et on note x \( \leqslant\) 0
- Quand on dit "positif strict " en Français,
en Mathématiques on note alors x \( > \) 0
- Quand on dit "négatif strict " en Français,
en Mathématiques on note alors x \( < \) 0
- En Français, on peut dire que 0 est "positif" et "négatif" en même temps
0 \( \leqslant\) 0 et 0 \( \geqslant\) 0
- ORDRE

- Les nombres entiers relatifs sont rangés dans l'ordre croissant de gauche à droite sur la droite discrète des nombres entiers relatifs et dans l'ordre décroissant de droite à gauche.
(Partout sur cette droite, on a des nombres de plus en plus grands quand on se déplace vers la droite,
et des nombres de plus en plus petits quand on se déplace vers la gauche).
- Des nombres ENTIERS RELATIFS aussi GRANDS QUE L'ON VEUT :

Quand on va très loin vers la droite, on obtient des nombres très grands comme par exemple.
- Des nombres ENTIERS RELATIFS aussi PETITS QUE L'ON VEUT :
Quand on va très loin vers la gauche, on a des nombres très petits et négatifs qui sont pourtant très éloignés de 0 (ils ont une grande valeur absolue mais sont très petits. La valeur absolue d'un nombre est sa distance à 0)

- -1 000 000 = -106 soit "moins un millions" est un nombre "négatif très petit"
- On écrit -∞ pour indiquer qu'il n'y a pas de plus petit nombre entier relatif négatif
- Vide et Zoom INUTILE
- Si on ZOOM entre 0 et 1 par exemple !
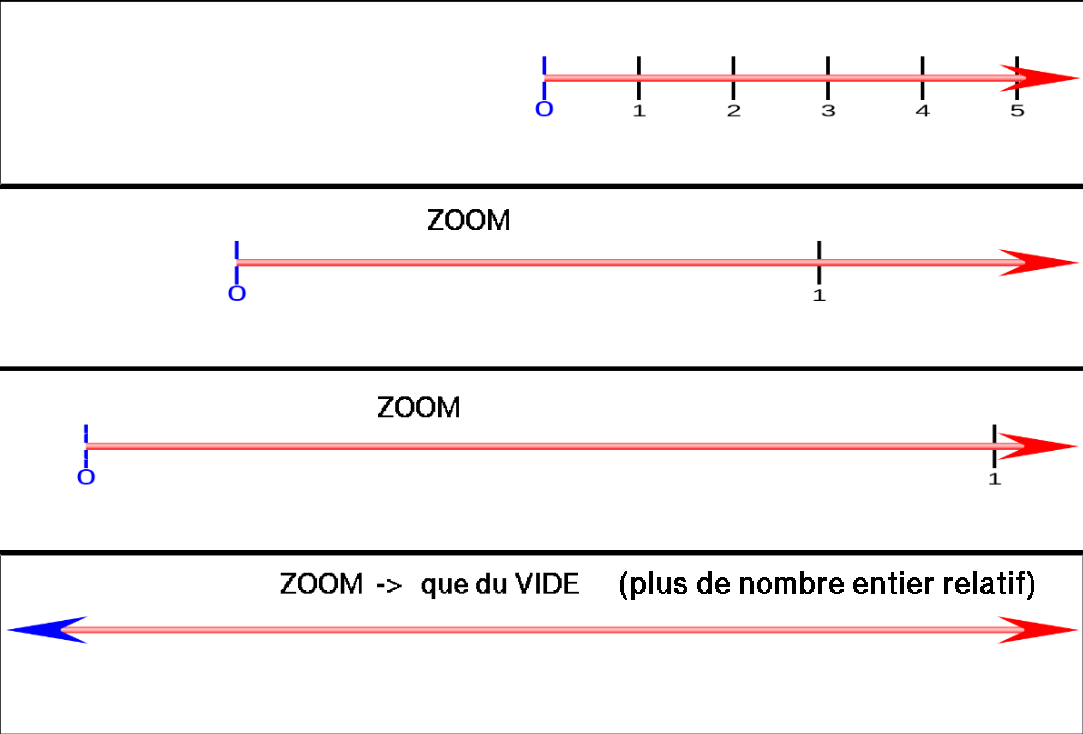
- Entre deux entiers relatifs successif, il n'y a aucun autre entier relatif strictement compris. (il y a du vide)






