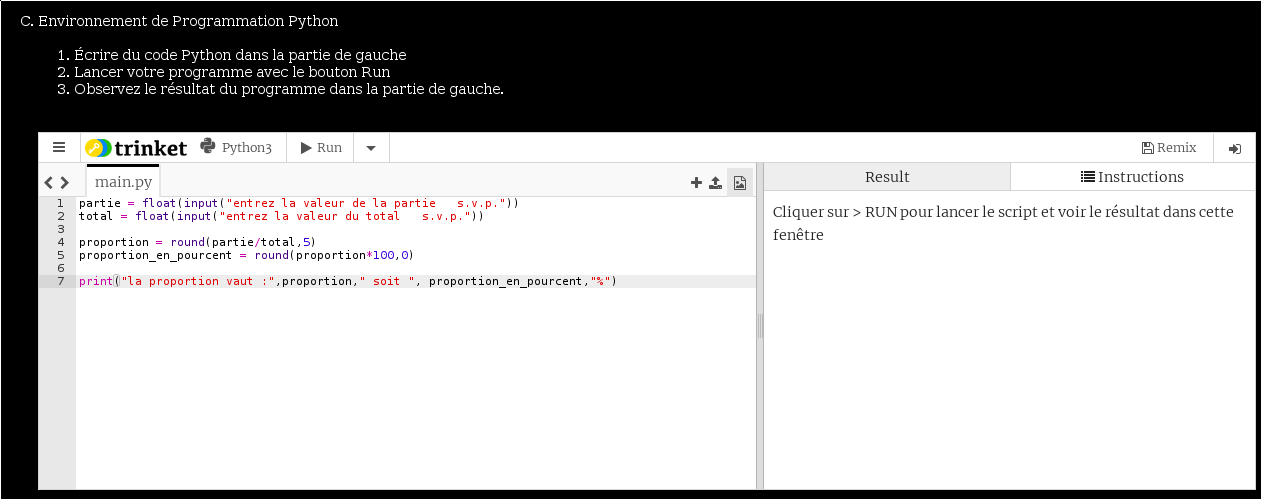
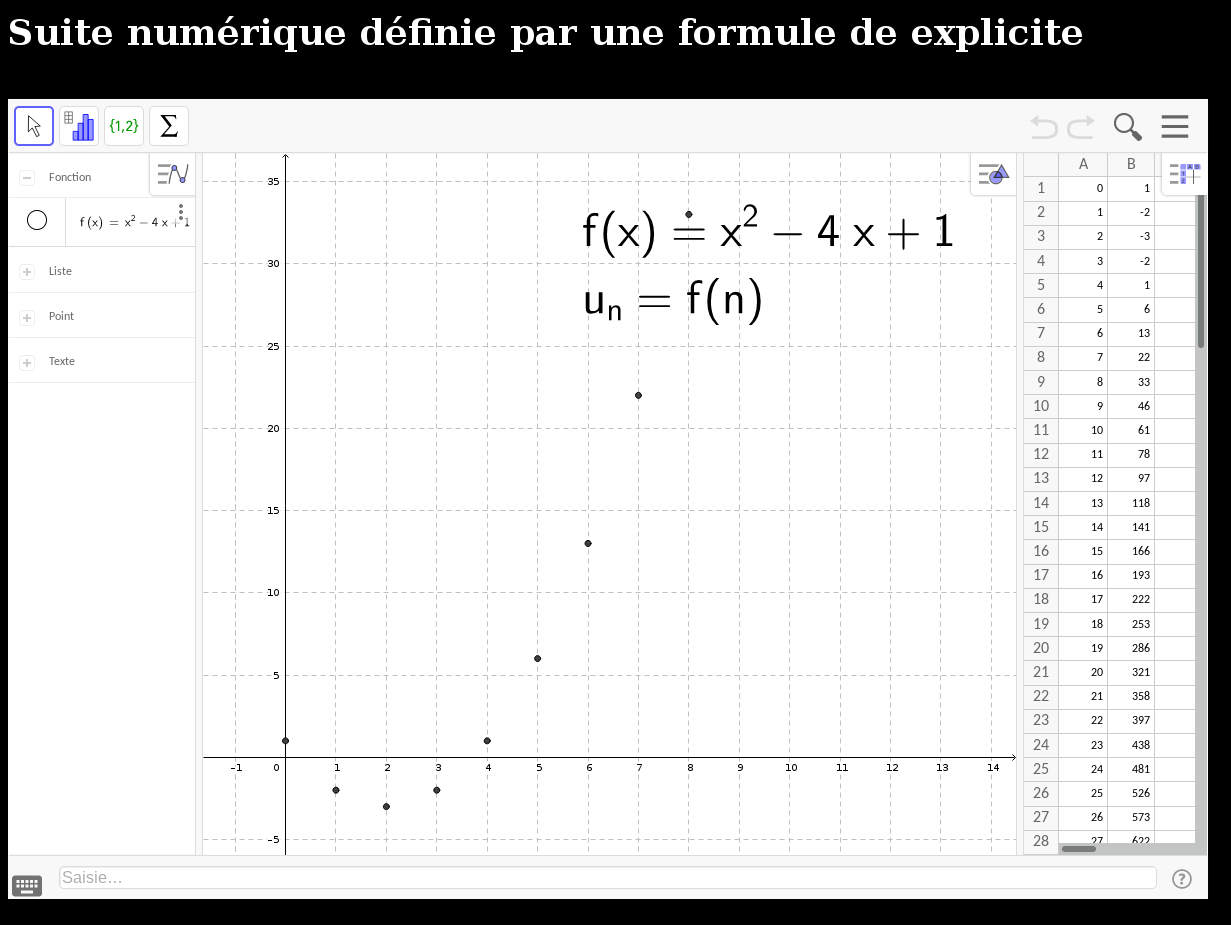
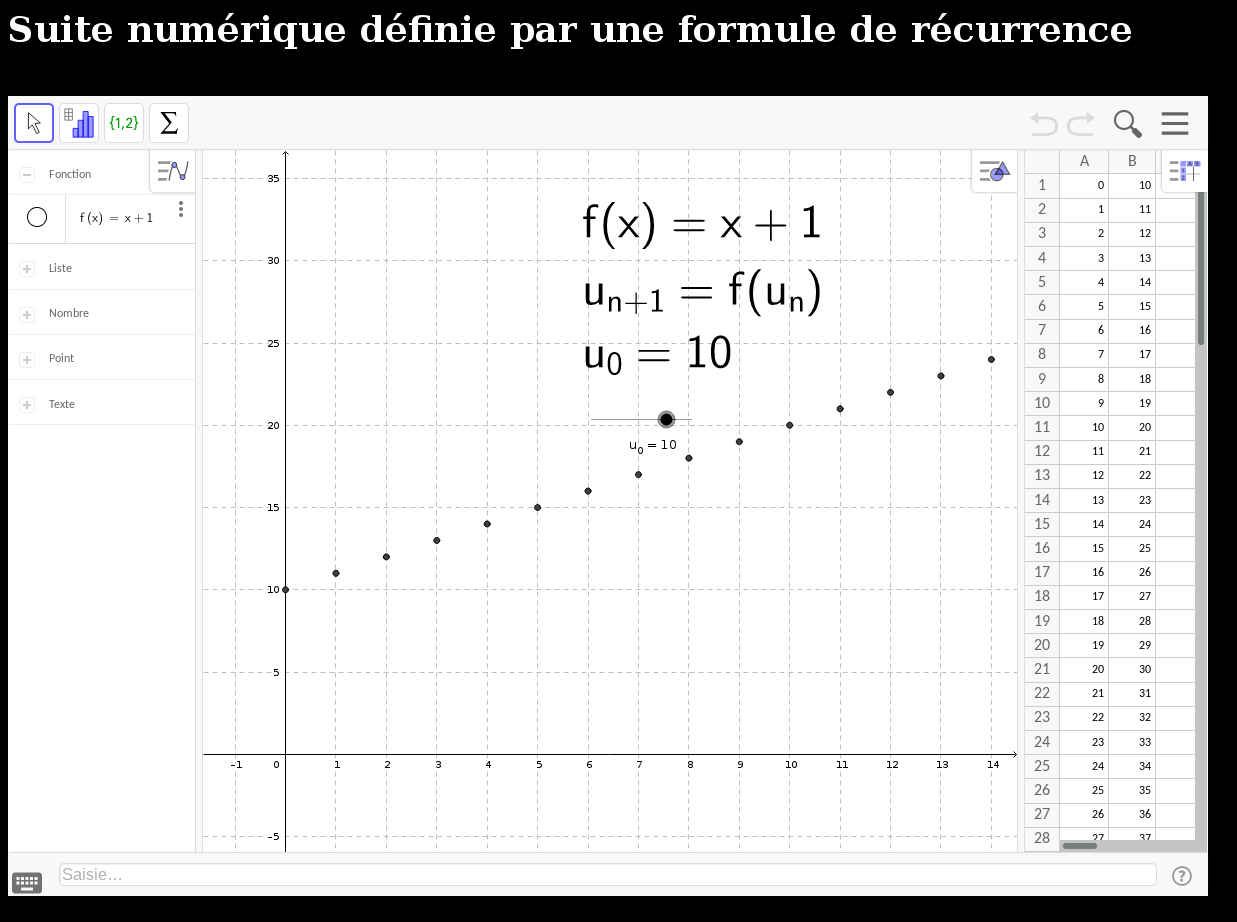
- cette page

- enigme_suite_geometrique_nenuphar $enigme_suite_geometrique_nenuphar
- enigme_suite_geometrique_feuille_papier_lune $enigme_suite_geometrique_feuille_papier_lune
- Multiplication de cellules

- Formule explicite (diaporama pdf)
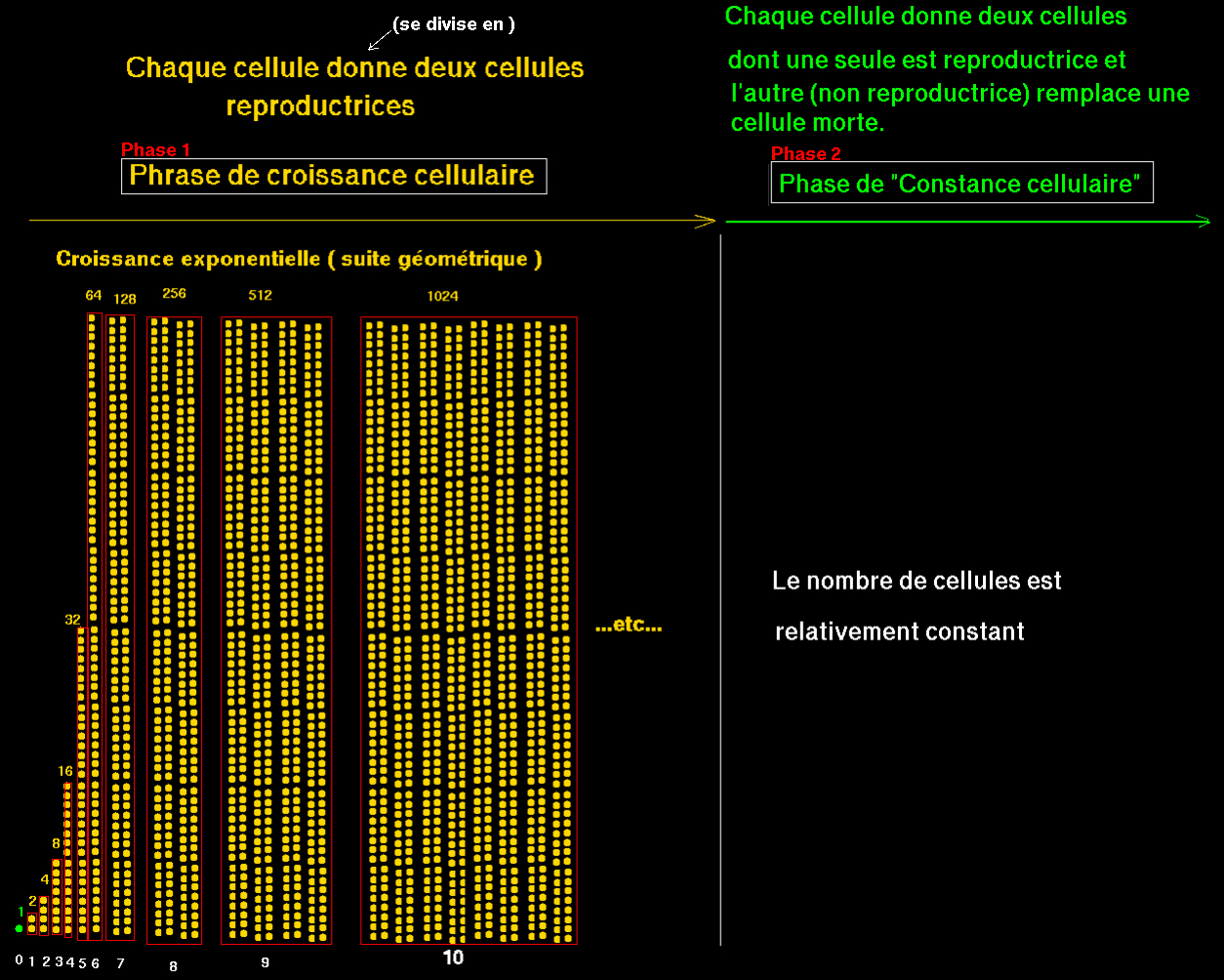



 animé
animé

 animé
animé

 animé
animé
 animé
animé
 animé
animé

 animé
animé

 animé
animé
- Visualisation (tableur)
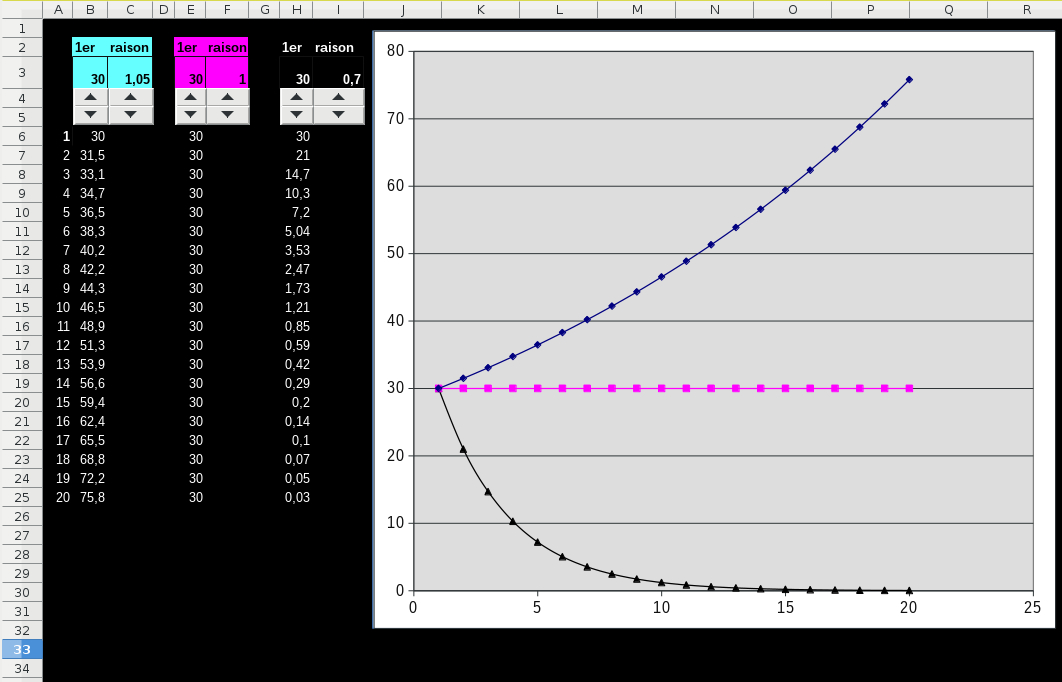
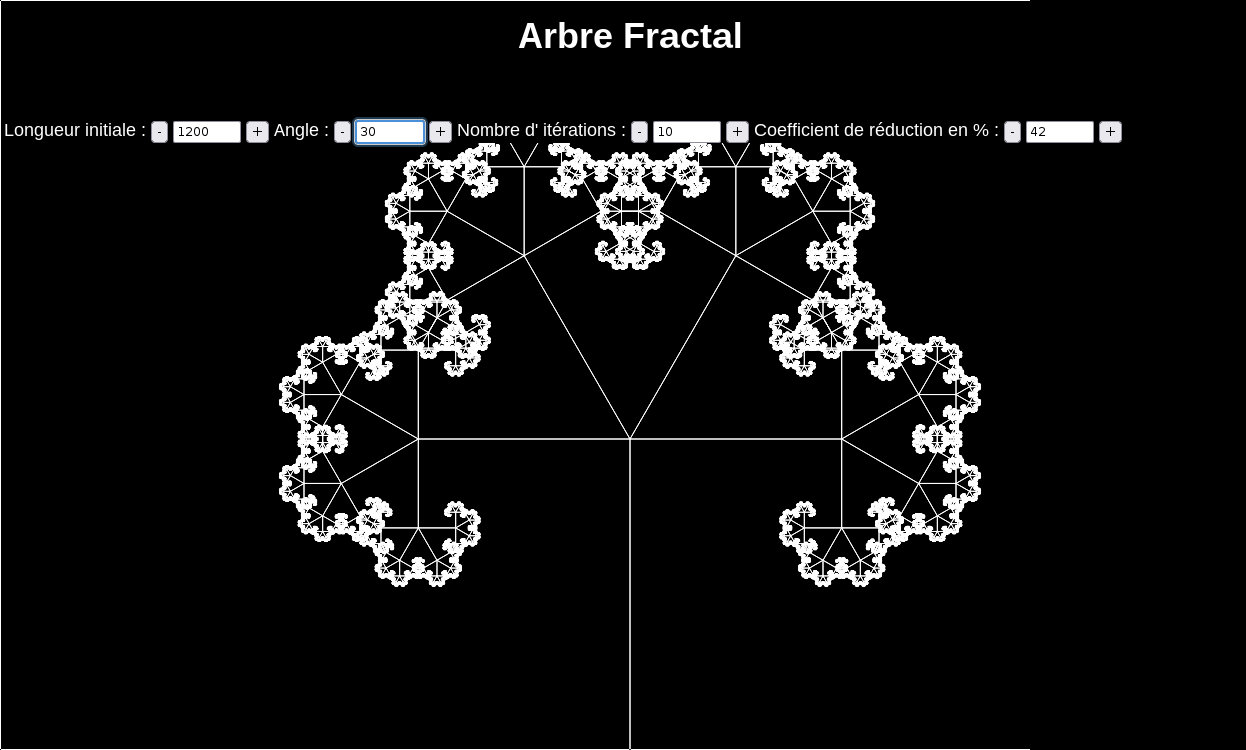
- Visualisation (html)

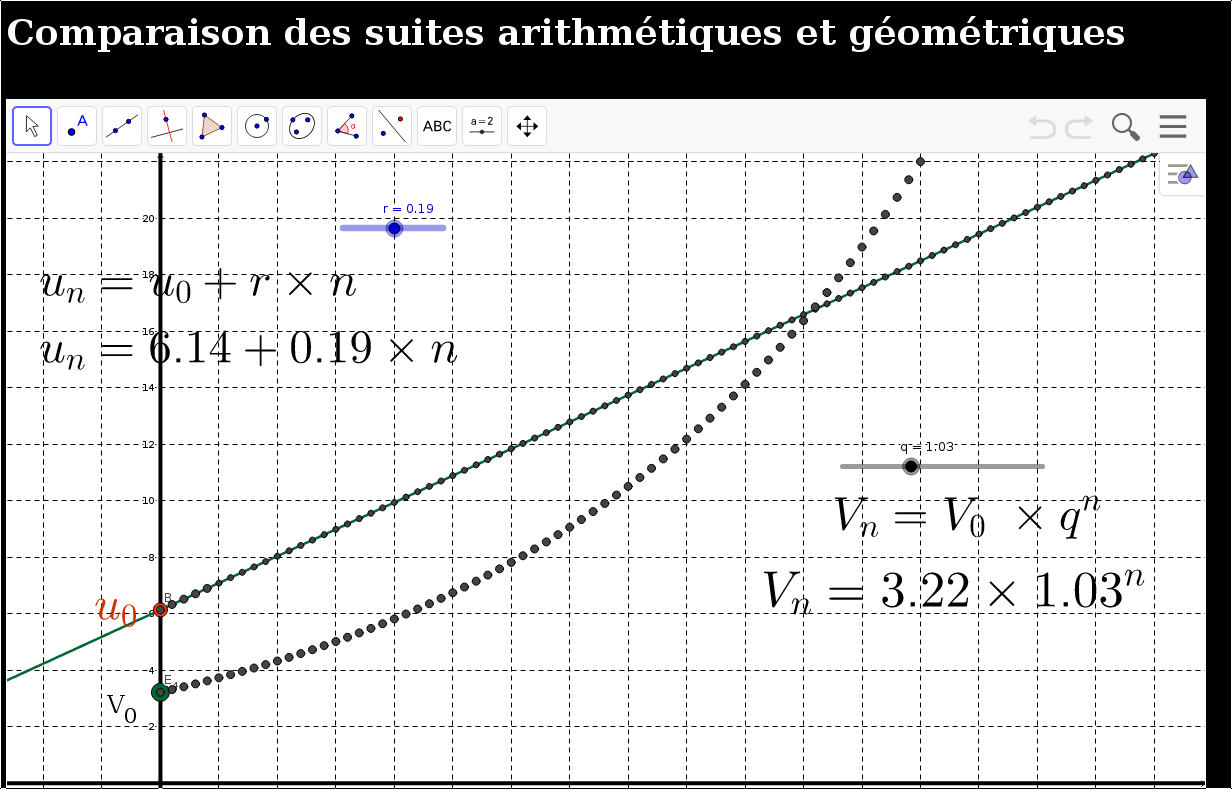
- Comparaison Suite Arithmétique, Suite Géométrique (html)
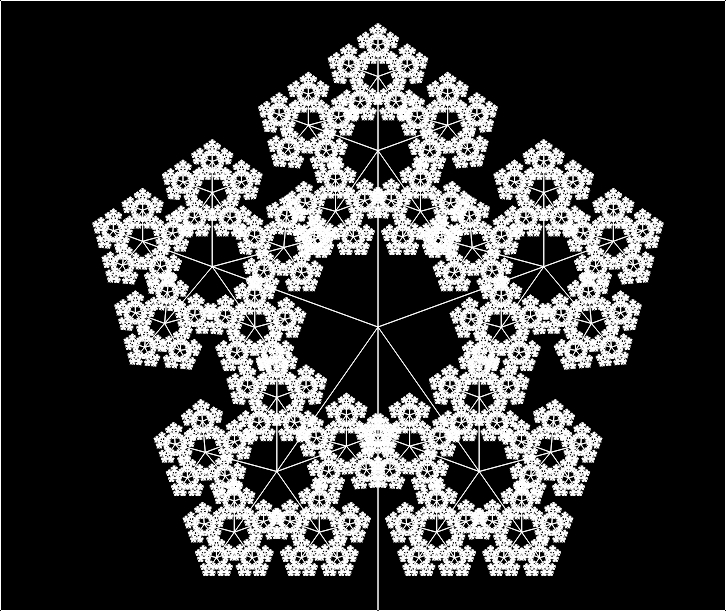
- Spirale géométrique (html)

- Spirale géométrique animée (html)
- Flocon de Koch (html)

- Flocon de Koch avec réduction (html)

- Somme des termes (html)

- *qcm_preliminaire_suites_geometriques $qcm_preliminaire_suites_geometriques
-
☺
- *calculs_suites_geometriques $calculs_suites_geometriques
- *calculs_a_partir_d_une_histoire_geometrique $calculs_a_partir_d_une_histoire_geometrique
- *exercice_preliminaire_complet_g $exercice_preliminaire_complet_g
- *exercice_preliminaire_complet_2_g $exercice_preliminaire_complet_2_g
- * exercice_preliminaire_complet_3_g $exercice_preliminaire_complet_3_g
- * reconnaitre_une_suite_geometrique_g $reconnaitre_une_suite_geometrique_g
- *premier_terme_et_raison_g $premier_terme_et_raison_g
- *calcul_de_termes_g $calcul_de_termes_g
- *calcul_de_termes_2_g $calcul_de_termes_2_g
- *calcul_de_termes_3_g $calcul_de_termes_3_g
- *calcul_de_termes_4_g $calcul_de_termes_4_g
- *calcul_de_termes_5_g $calcul_de_termes_5_g
- *calcul_de_termes_et_formule_explicite_g $calcul_de_termes_et_formule_explicite_g
- *trouver_la_formule_suites_geometriques $trouver_la_formule_suites_geometriques
- * formule_explicite_g $formule_explicite_g
- *formule_de_recurrence_g $formule_de_recurrence_g
- * tableur_g $tableur_g
- tableur_g_sur_pc $tableur_g_sur_pc
- equation_a_puissance_x_egal_b $equation_a_puissance_x_egal_b
- equation_a_fois_b_puissance_x_egal_c $equation_a_fois_b_puissance_x_egal_c
- equation_a_fois_b_puissance_x_plus_d_egal_e $equation_a_fois_b_puissance_x_plus_d_egal_e
- *determination_du_rang_pour_depasser_un_seuil_g $determination_du_rang_pour_depasser_un_seuil_g
- *comparaison_de_suites_g $comparaison_de_suites_g
- *sens_de_variation_g $sens_de_variation_g_g
- *courbe_g $courbe_g
- * cours_suites_geometriques $cours_suites_geometriques
- cours_suites_geometriques_plus_complet $cours_suites_geometriques_plus_complet
- cours_suites_geometriques_leger $cours_suites_geometriques_leger
- *suite_arithmetique_ou_geometrique $suite_arithmetique_ou_geometrique
- *suites_geometriques_grille_a_cliquer $suites_geometriques_grille_a_cliquer
- tp_suites_geometriques $tp_suites_geometriques
- exercice_complet_suites_numeriques $exercice_complet_suites_numeriques
- tp_suites_geometriques_simplifie $tp_suites_geometriques_simplifie
- (tp) placement_interets_composes $placement_interets_composes
- arithmetique_ou_geometrique $arithmetique_ou_geometrique
- *somme_des_termes_g $somme_des_termes_g
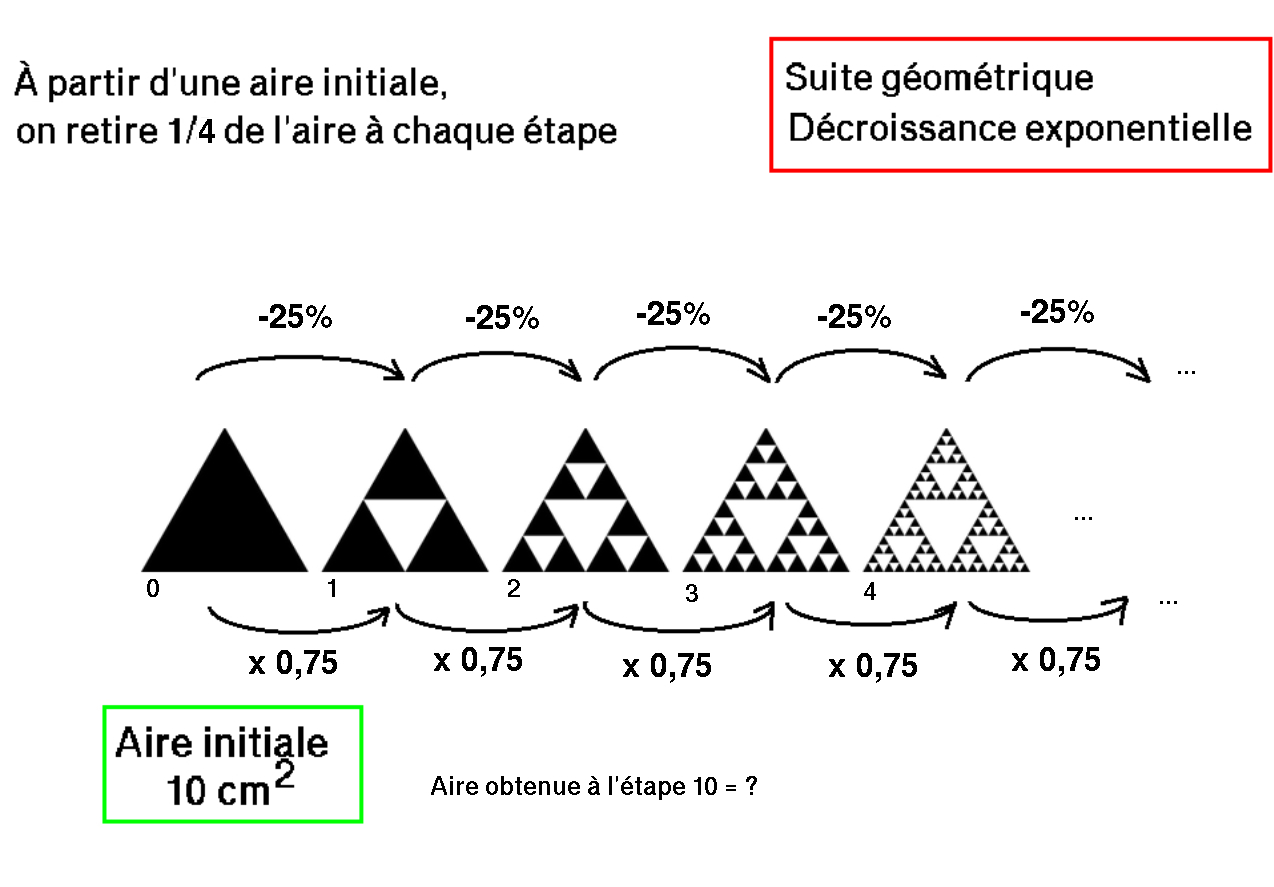
les suites géométriques servent à "modéliser" une situation où une "chose" (poids, taille, population, ...)
augmente ou diminue "régulièrement en pourcentage " (augmente de 10% tous les jours, ou diminue de 20% tous les mois, ...),
à partir d'une valeur initiale (valeur de départ, premier terme)
Il faut avant toutes choses, savoir faire des calculs simples faisant intervenir les opérations :
× multiplication, / division, puissance 2, puissance 3, ... , puissance n.
☺
Il est important, quand on rencontre une suite numérique,
de savoir reconnaître une suite de nature géométrique,
et aussi, de savoir préciser la raison et le premier terme de la suite géométrique
☺
Il faut maintenant savoir calculer un terme quelconque de la suite,
dès lors que l'on connaît le premier terme et la raison de la suite,
ceci, quand la suite est croissante ou décroissante,
mais aussi, quand on donne un nom aux termes de la suite,
de même, quand on ne part pas du premier terme
☺
Une application concrète, où l'on doit calculer des termes et trouver une formule explicite générale
☺
Pour s'entraîner à trouver la formule explicite générale,
dans un cas concrèt ou non.
☺
Pour s'entraîner à trouver la formule de récurrence,
et voir son utilité ainsi que celle de la formule explicite lorsqu'on utilise un tableur
☺
Il est maintenant temps de savoir déterminer la valeur du rang
à partir duquel la suite dépasse une certaine valeur (un certain seuil)
Cela nécéssite dans un premier temps de savoir résoudre des équations exponentielles basiques
une fois que l'on sait résoudre les équations précédentes, on peut revenir aux suites
et déterminer le rang à partir duquel on dépasse un certain seuil
mais aussi le rang à partir duquel une suite en dépasse une autre
☺
Pour reconnaître le sens de variation d'une suite (croissante, décroissante ou constante)
☺
Pour reconnaître une suite géométrique, quand on voit une courbe
☺
Il faut maintenant faire un bilan "complet" sur le chapitre,
ainsi que des "exercices complets"
☺
Un petit bonus sur la somme des termes d'une suite géométrique
- test_suites_geometriques_0 $test_suites_geometriques_0
bilan :
-
Votre moyenne (exercices avec *) est de : $moyenne_suites_geometriques