Cours : Nombre Pair, Nombre Impair
Introduction
On conçoit aisément ce qu'est un nombre pair, un nombre impair, mais pour justifier certains résultats qui les concernent, il faut donner des définitions
Définition : Définition (Pair) :
Quel que soit le nombre entier relatif \(a \in \mathbb Z\).
\(a\) est pair
équivaut à
Il existe un entier relatif \(k \in \mathbb Z\) tel que \(a = 2k\)
Exemple :
\(10\) est pair car \(10=2 \times 5\)
\(-12\) est pair car \(-12=2 \times(-6)\)
\(34\) est pair car \(34=2 \times17\)
Remarque : (pensez à une justification)
Quel que soit le nombre entier relatif \(a \in \mathbb Z\), \(a\) est pair équivaut à \(a\) est un multiple de \(2\)
Quel que soit le nombre entier relatif \(a \in \mathbb Z\), \(a\) est pair équivaut à \(a\) est divisible par \(2\)
Quel que soit le nombre entier relatif \(a \in \mathbb Z\), \(a\) est pair équivaut à \(\dfrac{a}{2} \in \mathbb Z\)
Quel que soit le nombre entier relatif positif, \(a \in \mathbb Z\), \(a\) est pair équivaut à "le reste de la division euclidienne de \(a\) par \(2\) est nul"
Quel que soit le nombre entier relatif \(a \in \mathbb Z\), \(a\) est pair équivaut à \(a\) une écriture décimale dont la partie entière se termine par \(0,2,4,6,8\)
Exemple : contre-exemple
13 n'est pas pair car il ne se termine pas par 0,2,4,6 ou 8
Définition : Définition (Impair) :
Quel que soit le nombre entier relatif \(a \in \mathbb Z\).
\(a\) est impair
équivaut à
Il existe un entier relatif \(k \in \mathbb Z\) tel que \(a = 2k + 1\)
Exemple :
\(11\) est impair car \(11=2 \times 5 +1\)
\(-35\) est impair car \(-35=2 \times (-18)+1\)
Remarque : (pensez à une justification)
Quel que soit le nombre entier relatif positif \(a \in \mathbb Z\), \(a\) est impair équivaut à "le reste de la division euclidienne de \(a\) par \(2\) est égal à \(1\)"
Quel que soit le nombre entier relatif positif \(a \in \mathbb Z\), "le reste de la division euclidienne de \(a\) par \(2\) est ou bien égal à \(0\), ou bien égal à \(1\) et ceci exclusivement"
Ce qui signifie qu'un entier relatif positif quelconque est ou bien pair, ou bien impair et ceci exclusivement
On admettra qu'il en est de même pour tous les entiers relatifs
Attention : Propriété exemplaire
Propriété exemplaire ( nombre impair et carré )
Quel que soit le nombre entier relatif \(a \in Z\).
Si "\(a\) est impair " Alors "\(a^2\) est impair "
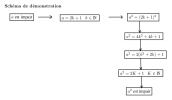
Complément : démonstration de la propriété précédente
Soit \(a\) un entier relatif quelconque (Supposons que : \(a\) soit impair, Montrons que : \(a^2\) est impair)
Supposons \(a\) impair
soit alors \(k \in \mathbb Z\) tel que \(a=2k+1\)
On a : \(a^2 = (2k+1)^2\)
donc : \(a^2 = (2k+1)(2k+1)\)
donc : \(a^2 = (2k+1)\times 2k + (2k+1)\times 1\) (distributivité)
donc : \(a^2 = 4k^2 + 2k + 2k+ 1\) (distributivité)
donc : \(a^2 = 4k^2 + 4k+ 1\)
donc : \(a^2 = 2(\underbrace{2k^2+ 2k}_{K} )+ 1\) (2 en facteur)
donc : \(a^2 = 2K + 1\)
donc : il existe un entier relatif \(K\) tel que \(a^2 = 2K+1\)
donc \(a^2\) est impair
Quel que soit le nombre entier relatif \(a \in Z\).
Si "\(a\) est impair " Alors "\(a^2\) est impair "