- pente d'une droite (htm)
- Pente d'une route (pdf)
- Pente d'une droite (pdf)(diaporama)
- pente d'une droite (ggb) (html)
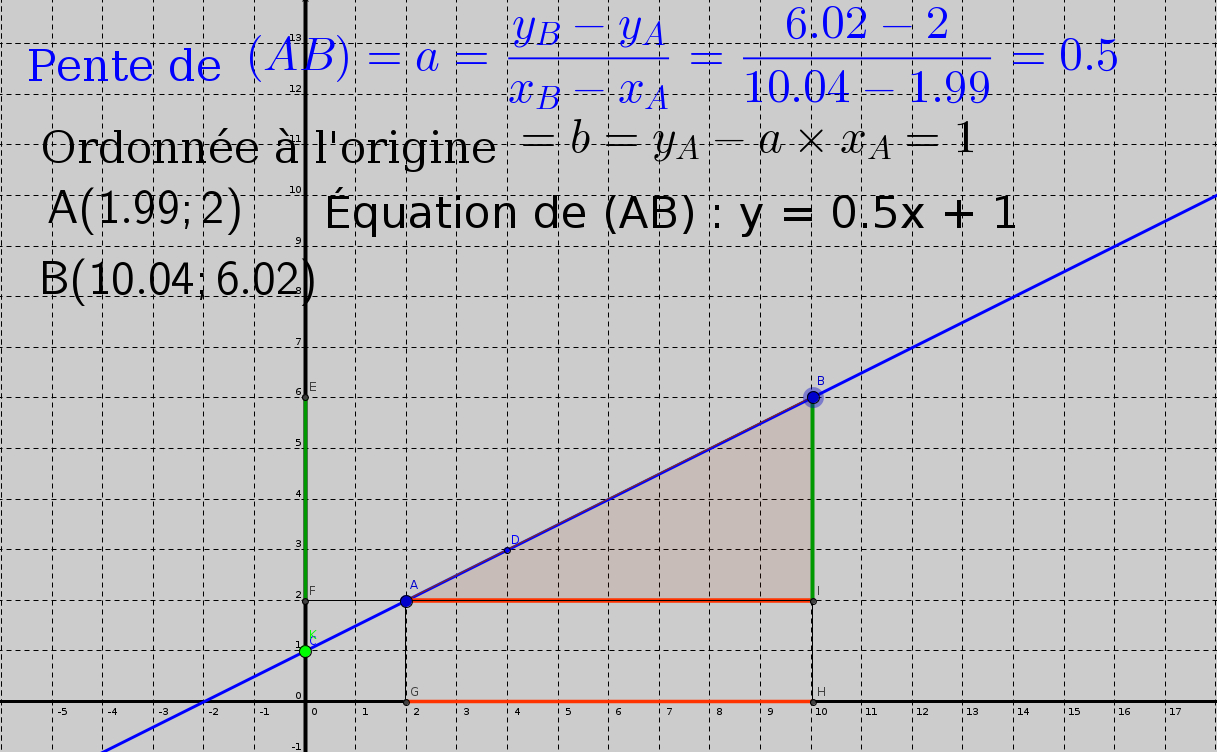
- pente route vélo (htm)
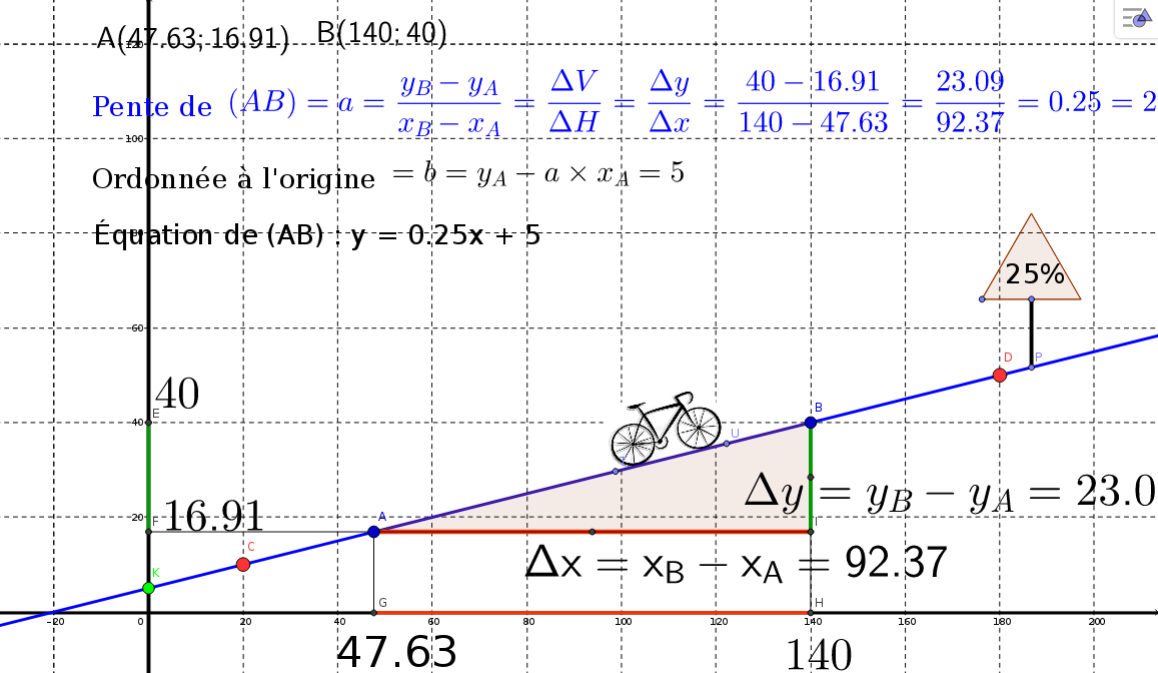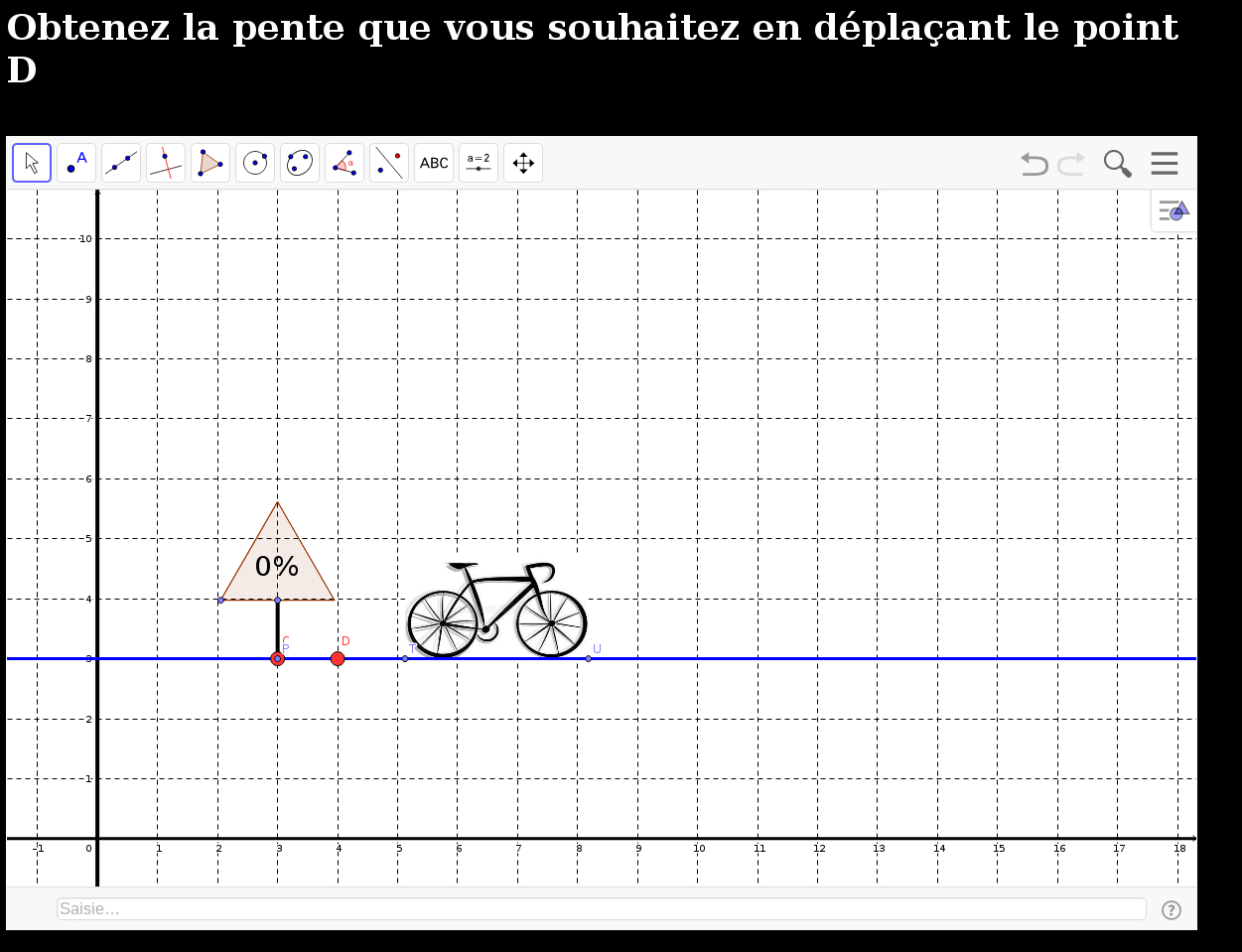
(ggb) - pente droite simplifié (htm)
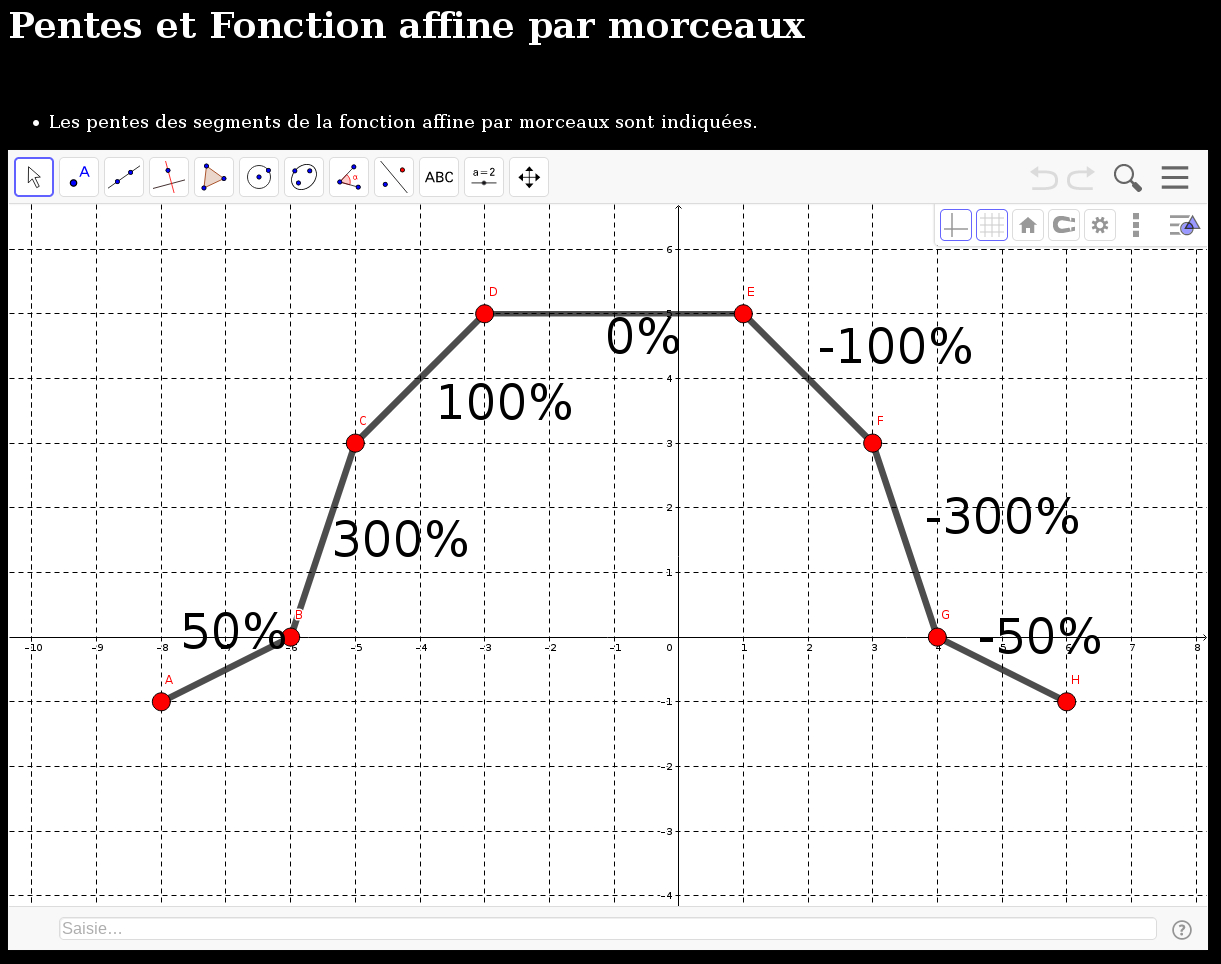
- Pente fonction affine par morceaux (htm)
- Taux de variatrion d'une fonction (htm)
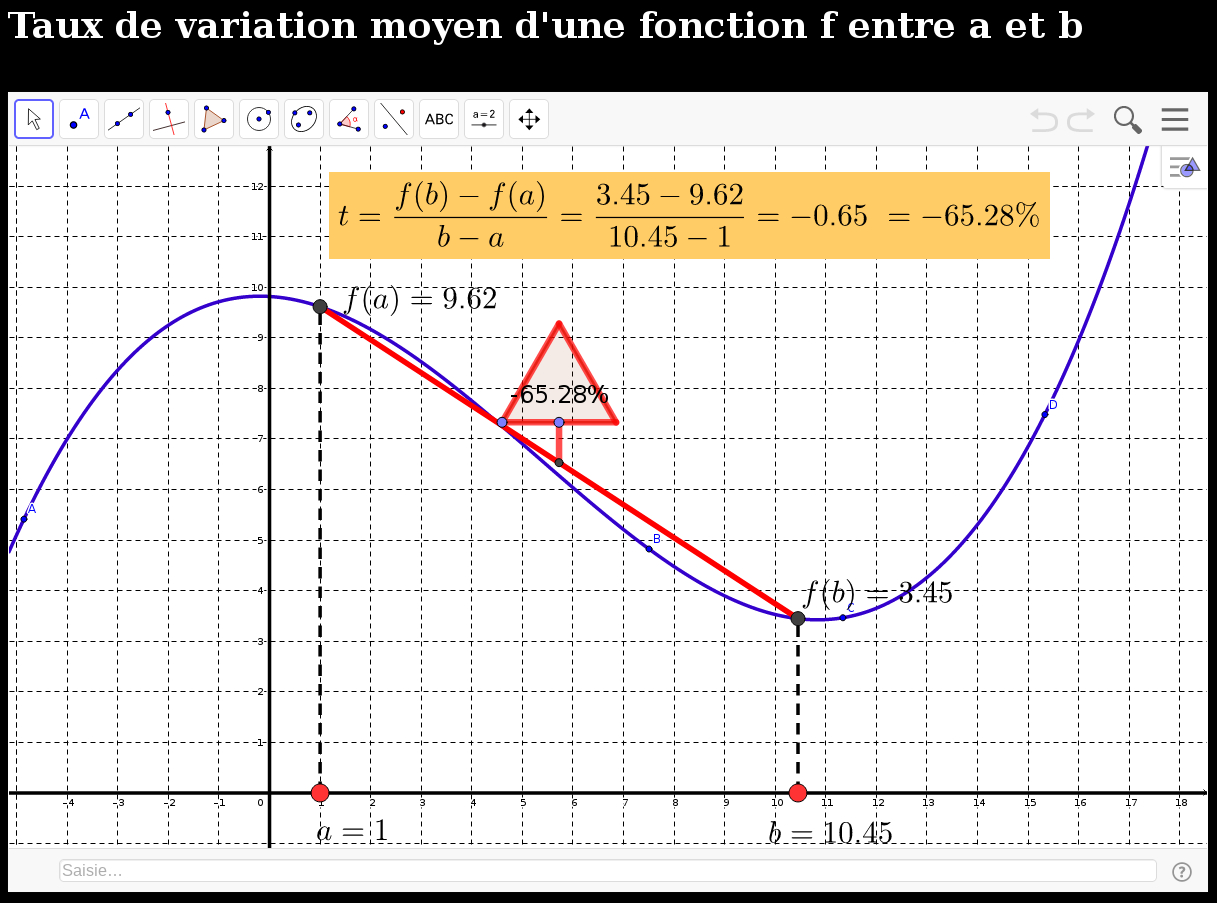
- Taux de variatrion d'une fonction entre a et a+h (htm)
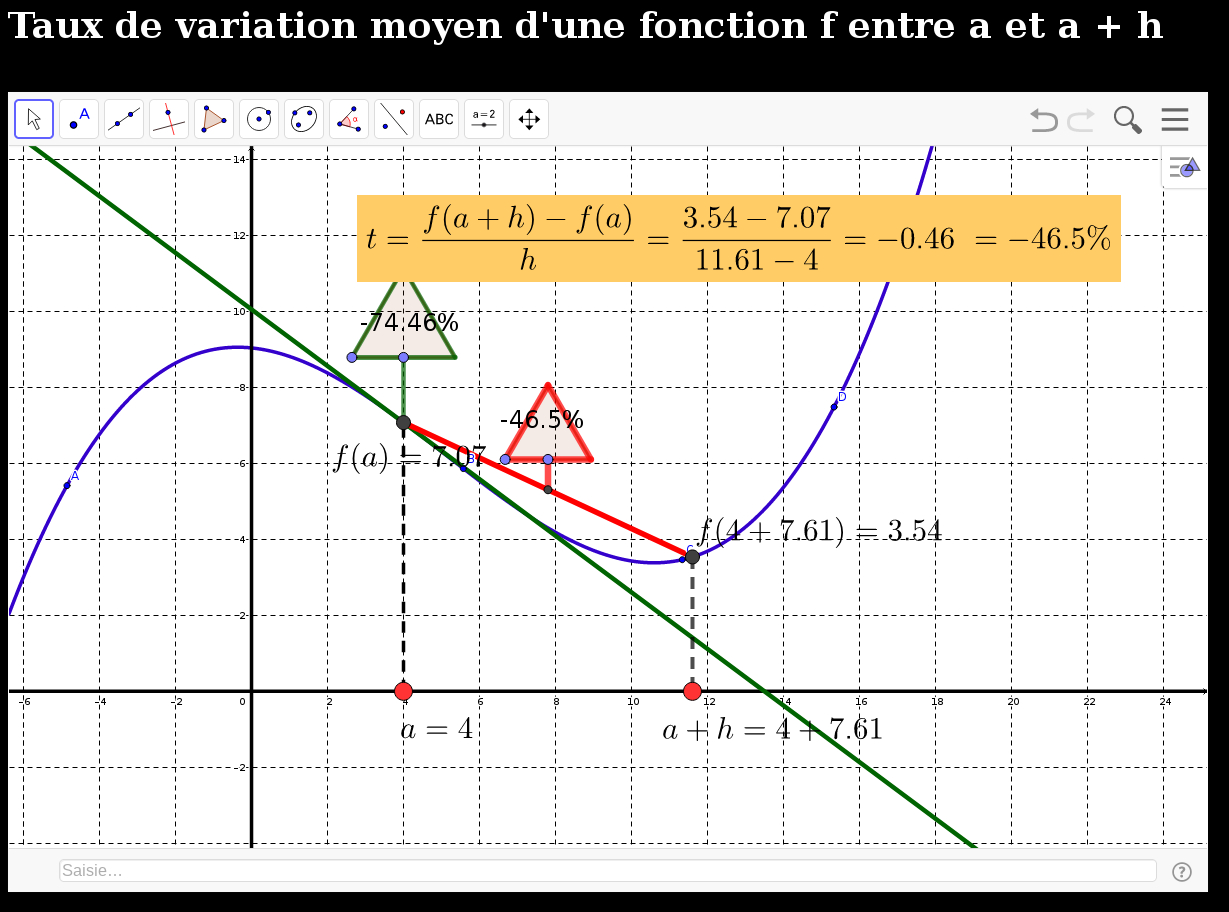
- sécante et tangente (ggb) (html)
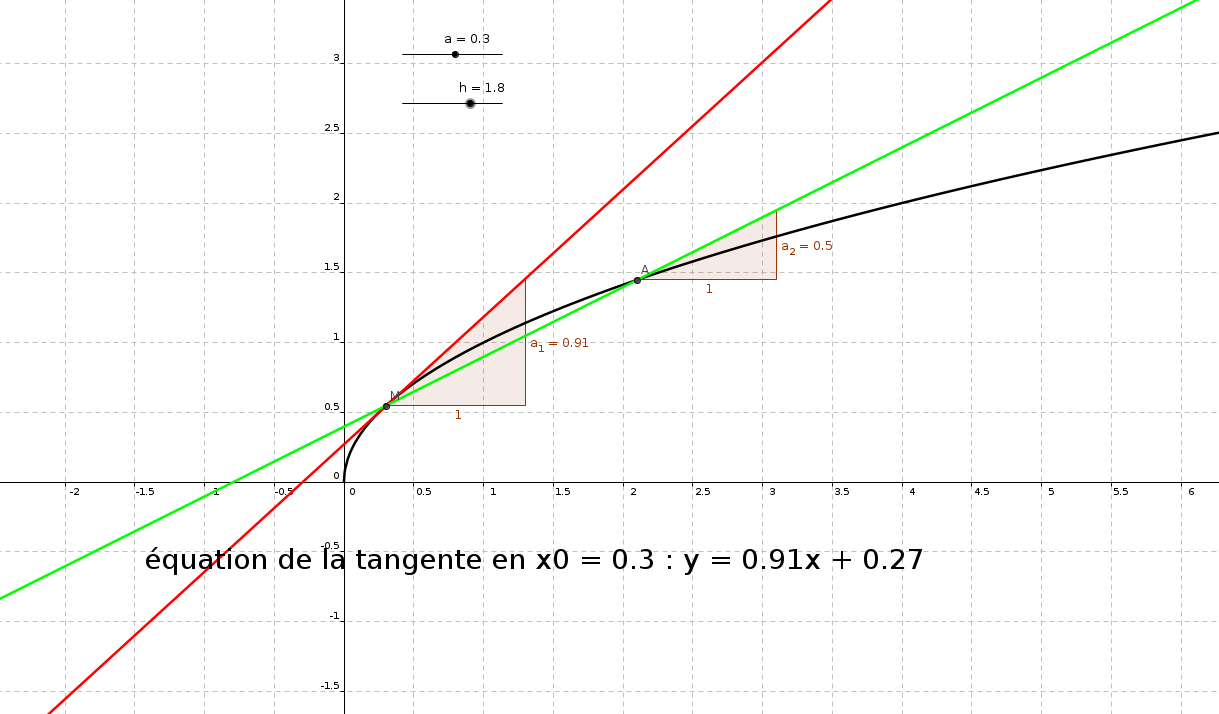
- pente courbe (htm)
(ggb) - pente courbe simplifiée (htm)
- pente courbe et lecture graphique (htm)
- Fonction et sa dérivée (htm)
(ggb) (video webm) - Variations de la fonction et signe de sa dérivée (htm)
(ggb) (video webm) (video "cours" webm) - visualisation (xls)
- courbe tangente convexité (html)
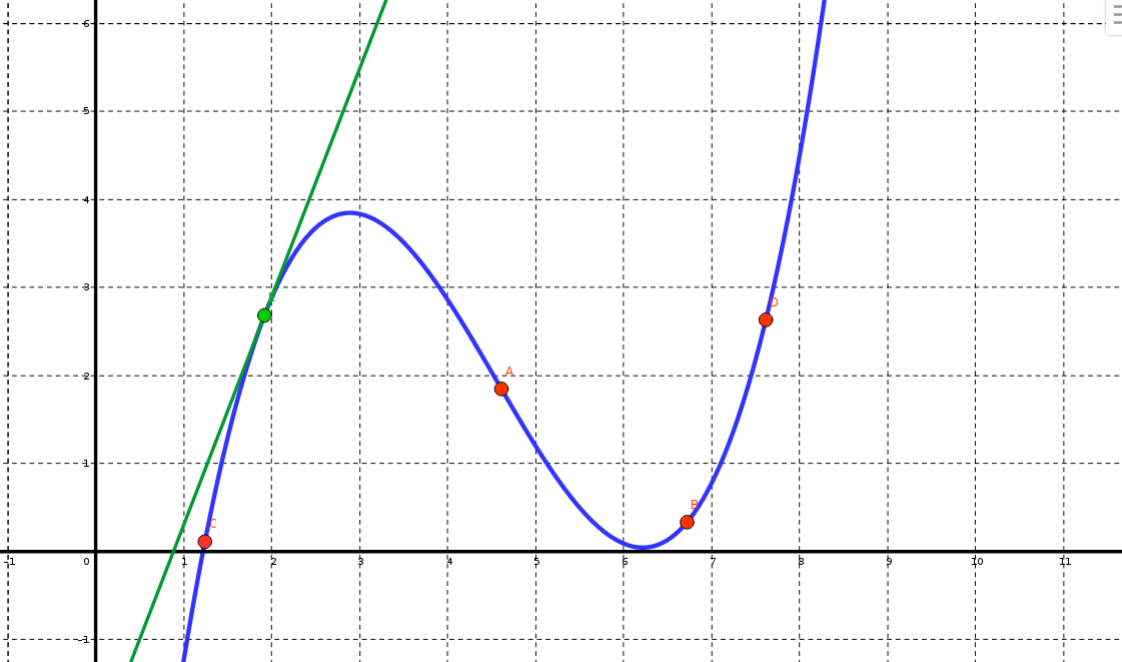( ggb) - formule de fonction et convexité (html)
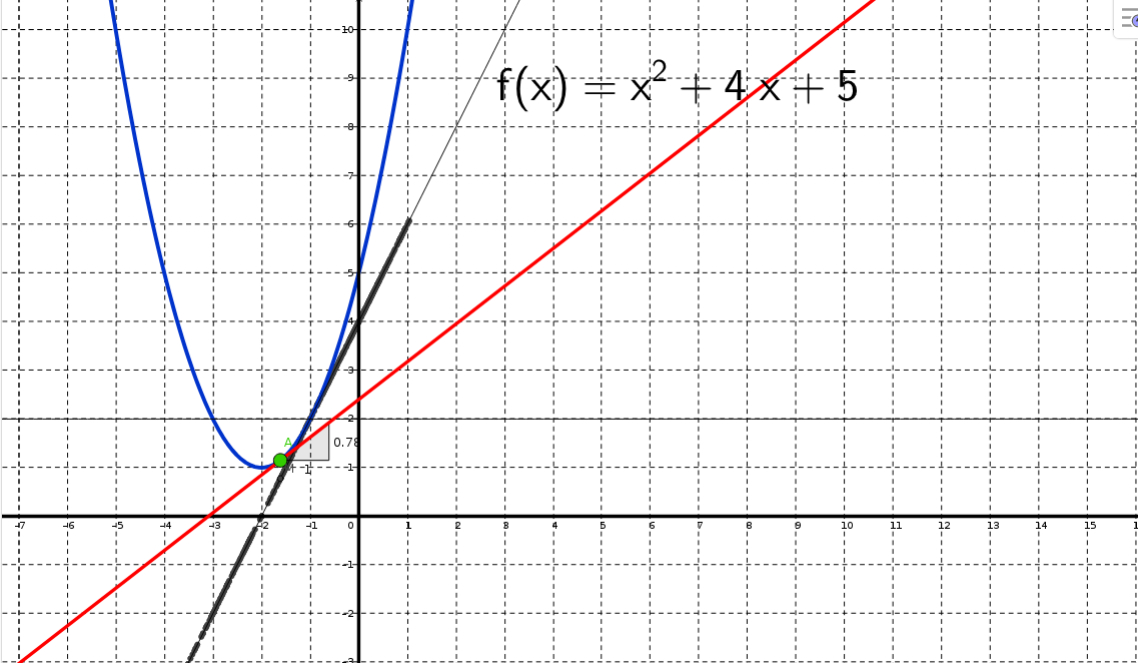( ggb)
- un cours détaillé (pdf)
- feuille d'un ensemble de savoir-faire (html)
- calcul de dérivées (diaporama)
(document pdf) (corrigé pdf) - signe d'un binôme ax + b : (diaporama)
(document pdf) (corrigé pdf) - signe d'un produit de deux binômes (ax + b)(cx + d) : (diaporama)
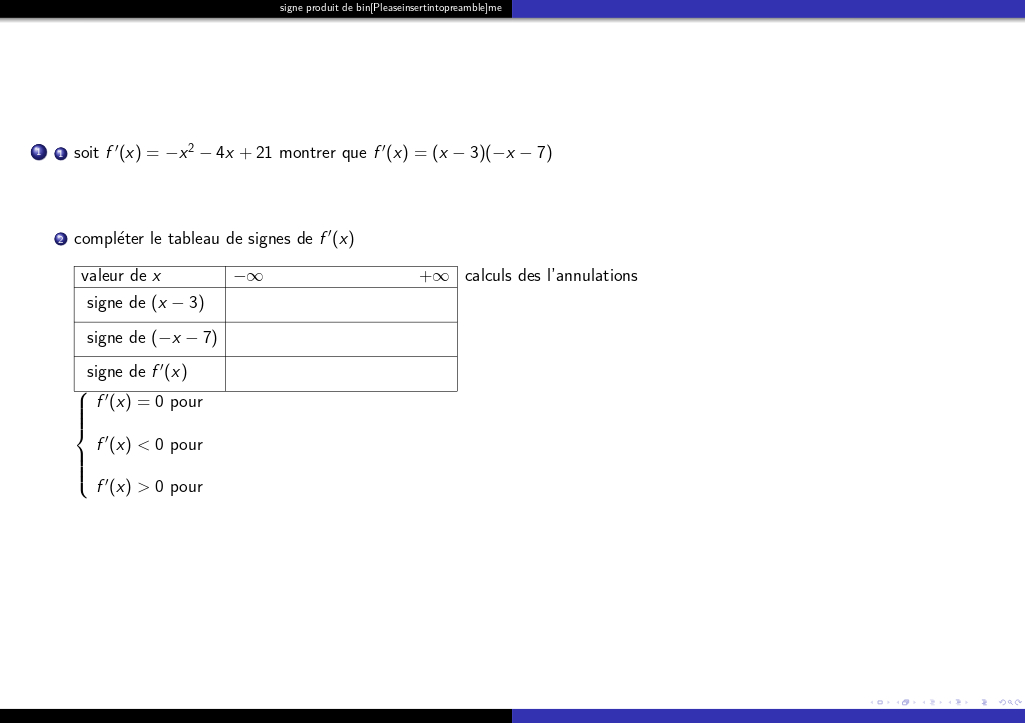(document pdf) (corrigé pdf) - signe d'un trinôme ax2 + bx + c : (diaporama)
(document pdf) (corrigé pdf) (hors programme pour les ST2S) - Étude des variations d'une fonction du second degré grâce à la dérivation : (diaporama)
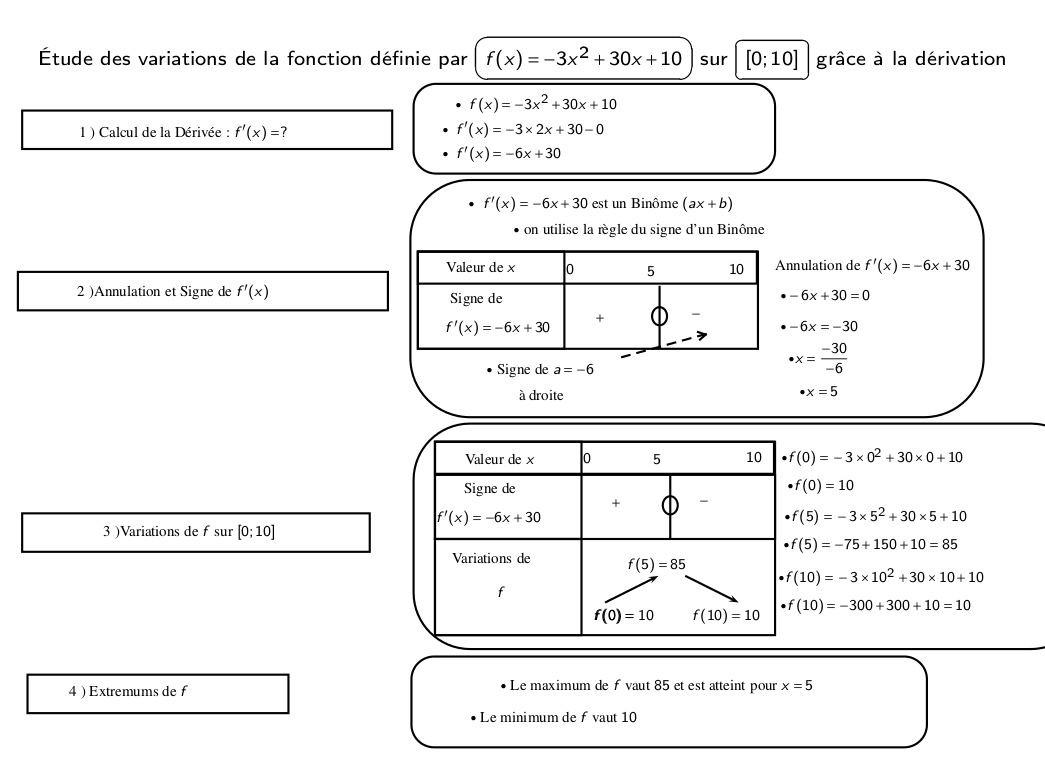
- Étude des variations d'une fonction du troisième degré grâce à la dérivation : (diaporama)
-
☺
- recherche_variations_de_la_droite_et_signe_de_la_pente $recherche_variations_de_la_droite_et_signe_de_la_pente
- regler_pente_droite $regler_pente_droite
- regler_pente_droite_100 $regler_pente_droite_100
- regler_pente_droite_200 $regler_pente_droite_200
- regler_pente_droite_m100 $regler_pente_droite_m100
- regler_pente_droite_m10 $regler_pente_droite_m10
- regler_pente_droite_m20 $regler_pente_droite_m20
- boucle_renforcement_pente_droite $boucle_renforcement_pente_droite
- boucle_renforcement_pente_droite_graphique $boucle_renforcement_pente_droite_graphique
- pente_droite $pente_droite
- construire_droite_pente $construire_droite_pente
- construire_droite_pente_2 $construire_droite_pente_2
- boucle_renforcement_pente_courbe_graphique $boucle_renforcement_pente_courbe_graphique
- construire_tangente_a_une_courbe_de_fonction $construire_tangente_a_une_courbe_de_fonction
- nombre_derive_et_tangente $nombre_derive_et_tangente
- lecture_nombre_derive_et_tangente_2 $lecture_nombre_derive_et_tangente_2
- nombre_derive_et_tangente_2 $nombre_derive_et_tangente_2
- placer_points_nombre_derive_et_tangente_3 $placer_points_nombre_derive_et_tangente_3
- equation_d_une_tangente_a_la_courbe $equation_d_une_tangente_a_la_courbe
- nombre_derive $nombre_derive
- boucle_renforcement_taux_de_variation_moyen_fonction_par_formule $boucle_renforcement_taux_de_variation_moyen_fonction_par_formule
- boucle_renforcement_taux_de_variation_moyen_fonction_entre_a_et_a_plus_h $boucle_renforcement_taux_de_variation_moyen_fonction_entre_a_et_a_plus_h
- boucle_renforcement_taux_de_variation_moyen_entre_a_et_a_plus_h_et_h_tend_vers_0 $boucle_renforcement_taux_de_variation_moyen_entre_a_et_a_plus_h_et_h_tend_vers_0
- boucle_renforcement_variations_fonction_et_signe_derivee $boucle_renforcement_variations_foncction_et_signe_derivee
- signe_de_la_derivee $signe_de_la_derivee
- signe_de_la_derivee_cas_2 $signe_de_la_derivee_cas_2
- nombre_derive_complet $nombre_derive_complet
- nombre_derive_complet_sans_equation_tangente $nombre_derive_complet_sans_equation_tangente
- test_de_renforcement_calcul_derivees $test_de_renforcement_calcul_derivees
- derivees_usuelles_0 $derivees_usuelles_0
- derivees_usuelles_1 $derivees_usuelles_1
- boucle de renforcement annulation du binôme $boucle_renforcement_signe_du_binome
- test_de_renforcement_signe_du_binome_2 $test_de_renforcement_signe_du_binome_2
- trouver le tableau de signes d'une fonction affine $evaluation_fonctions_affines_tableau_de_signes
- tableau_de_signes d'un produit de binômes $tableau_de_signes
- tableau_de_signes d'un produit de binômes_2 $tableau_de_signes_2
- plan_etude_fonction_derivation $plan_etude_fonction_derivation
- derivation_etude_variations_degre_2_1 $derivation_etude_variations_degre_2_1
- derivation_etude_variations_degre_2_2 $derivation_etude_variations_degre_2_2
- degre_3_derivation_cas_1_total $degre_3_derivation_cas_1_total
- degre_3_derivation_cas_2_total $degre_3_derivation_cas_2_total
- degre_3_derivation_cas_3_total $degre_3_derivation_cas_3_total
- derivation_etude_variations_degre_3_1 $derivation_etude_variations_degre_3_1
- derivation_etude_variations_degre_3_2 $derivation_etude_variations_degre_3_2
- derivation_etude_variations_degre_3_3 $derivation_etude_variations_degre_3_3
- probleme_optimisation_degre_2_derivation_1 $probleme_optimisation_degre_2_derivation_1
- probleme_optimisation_degre_2_derivation_2 $probleme_optimisation_degre_2_derivation_2
- probleme_optimisation_degre_2_derivation_3 $probleme_optimisation_degre_2_derivation_3
- probleme_degre_deux_derivation $probleme_degre_deux_derivation
- etude_degre_trois_variations_probleme $etude_degre_trois_variations_probleme
- probleme_optimisation_degre_3 $probleme_optimisation_degre_3
Les résultats de ce chapitre sur la "dérivation d'une fonction",
permettent d'étudier les variations d'une fonction dont on connaît la formule,
on peut ainsi trouver le tableau de variations de la fonction,
en déduire les valeurs exactes des extrèmums ( maximum, minimum) de la fonction,
et résoudre des problèmes d'optimisation.
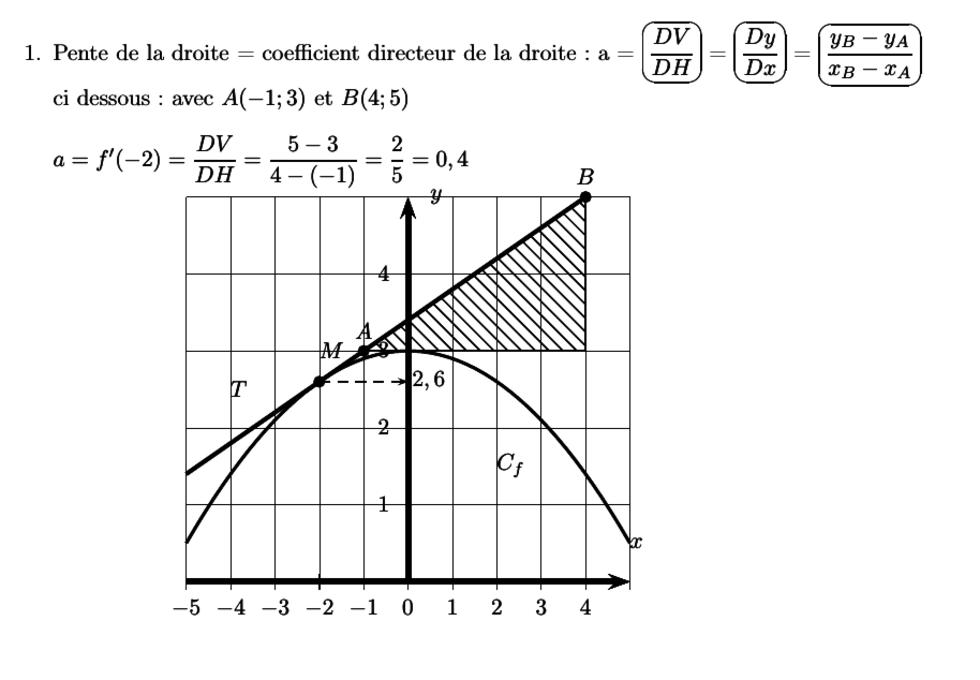
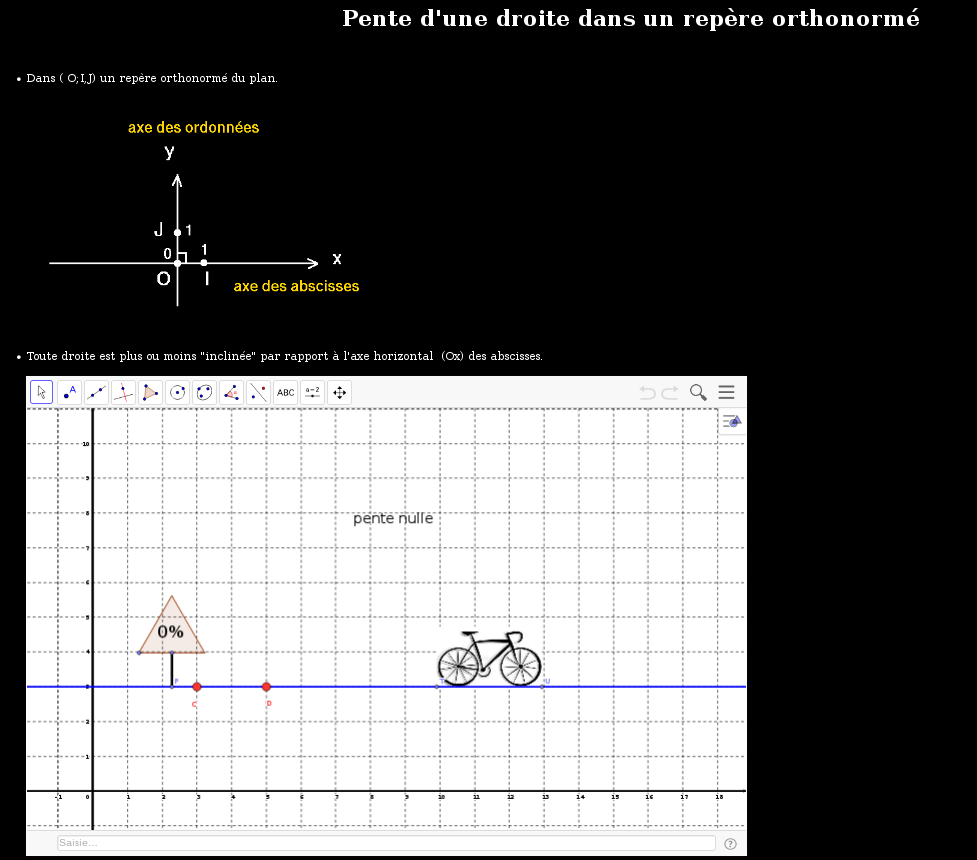
Dans un premier temps, il faut être capable de déterminer le coefficient directeur (ou pente) d'une droite,
dessinée dans un repère
ou encore,
dessiner une droite qui passe par un point donné et de pente donnée
☺
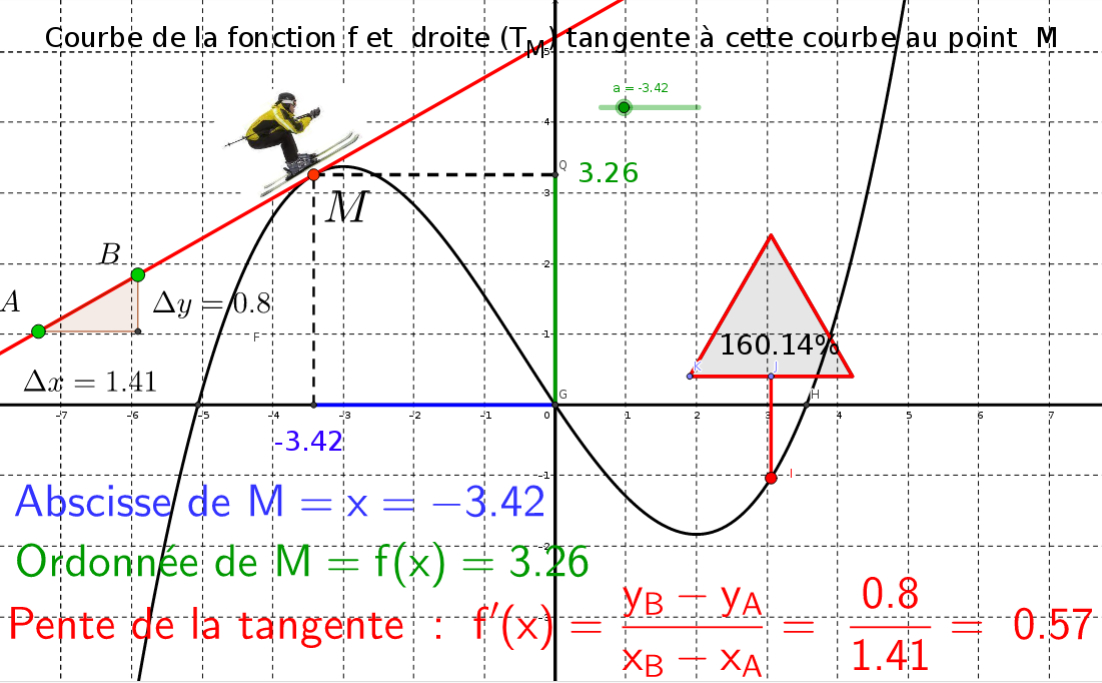
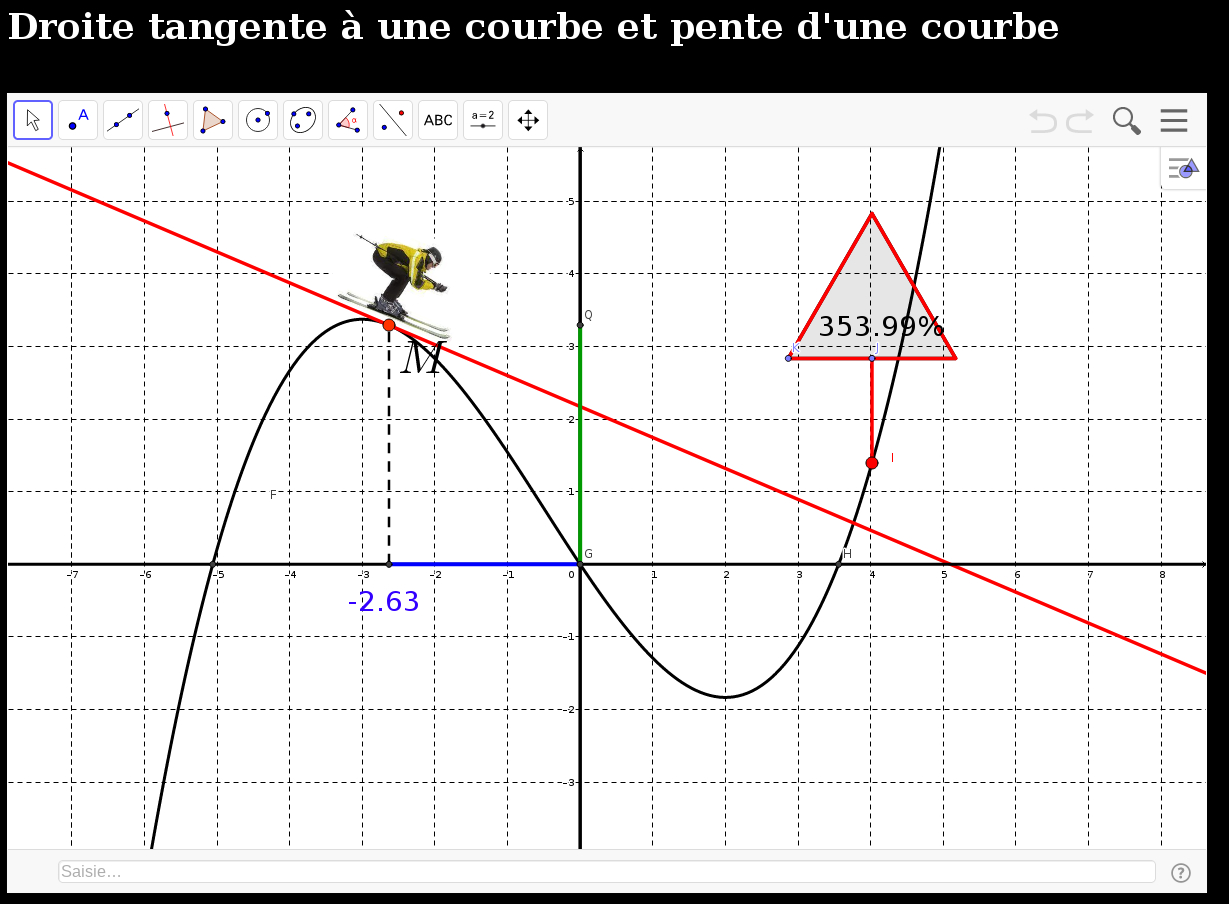
On peut maintenant déterminer graphiquement le coefficient directeur (ou pente),
d'une courbe (non droite) en un de ses points d'abscisse x0 noté f '(x0) à ne pas confondre avec
f (x0) qui est l'image de x0 par f.
(On détermine la pente de la courbe grâce à la droite tangente à la courbe au point considéré).
☺ceci pour la détermination de l'équation de la tangente à une courbe de fonction en un point donné
☺
On met en place la notion de taux de variation moyen d'une fonction entre deux points
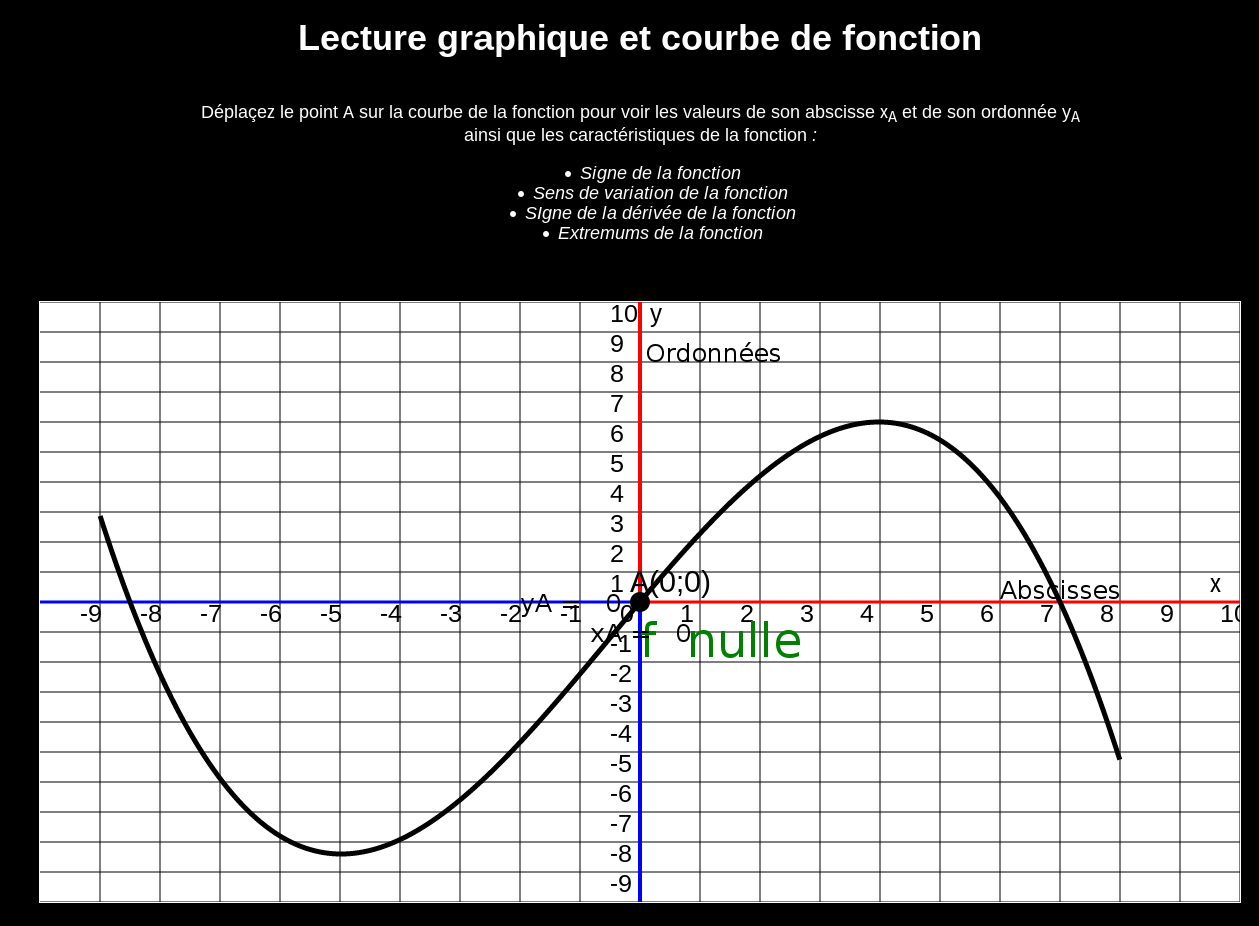
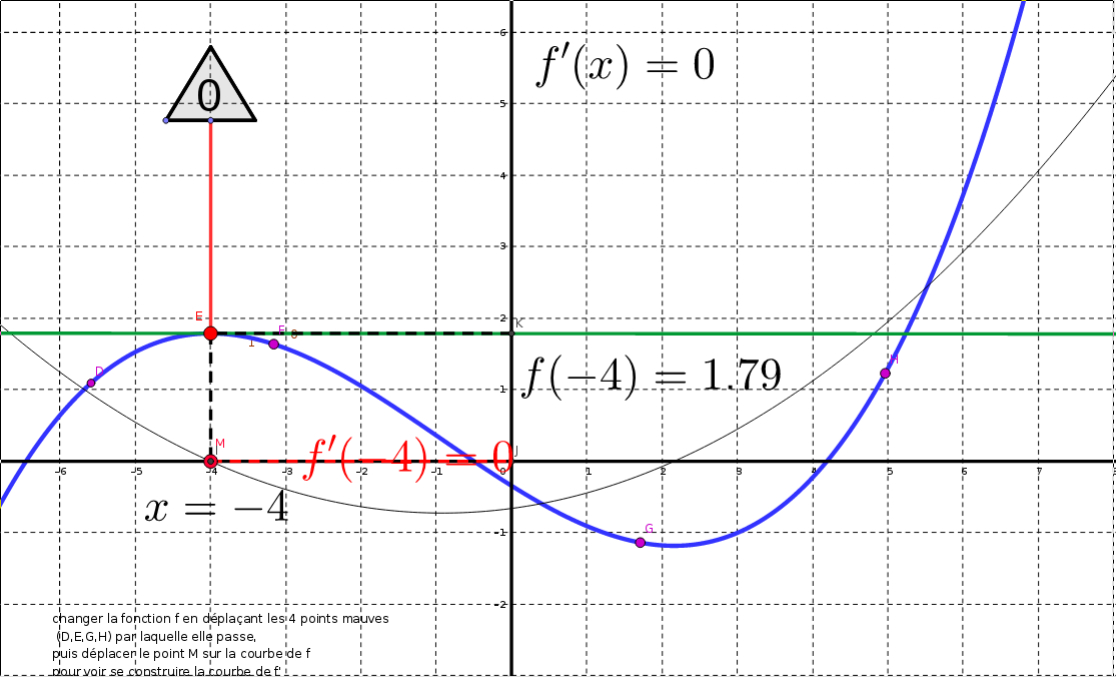
☺ Il est maintenant important de savoir déterminer le signe de la pente d'une courbe,
graphiquement . (autrement dit, on cherche le signe de f '(x) en fonction de x )
☺ On peut maintenant faire un bilan sur la partie "lecture graphique"
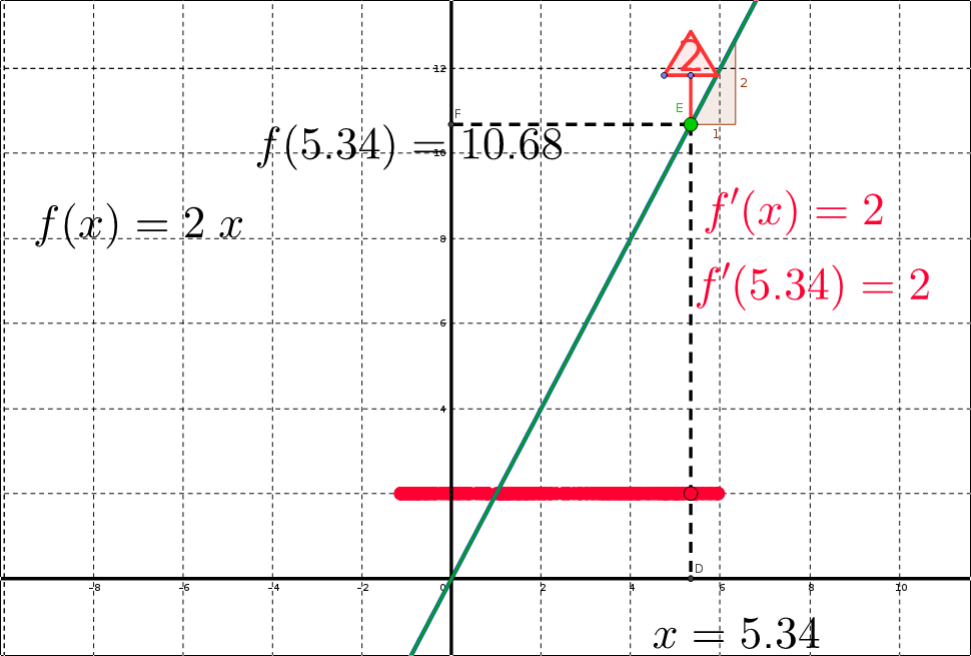
☺ Dans, cette partie, le coté algébrique est maintenant abordé,
il est très important de connaître par coeur les dérivées des fonctions usuelles
☺ Il faut maintenant être au point sur l'étude du signe d'une fonction affine,
ou d'un produit de fonctions affines
☺ voila !
on peut maintenant étudier les variations d'une fonction du second degré
grâce à la dérivation
☺ puis on s'intéresse à l'étude des variations d'une fonction du troisième degré
grâce à la dérivation
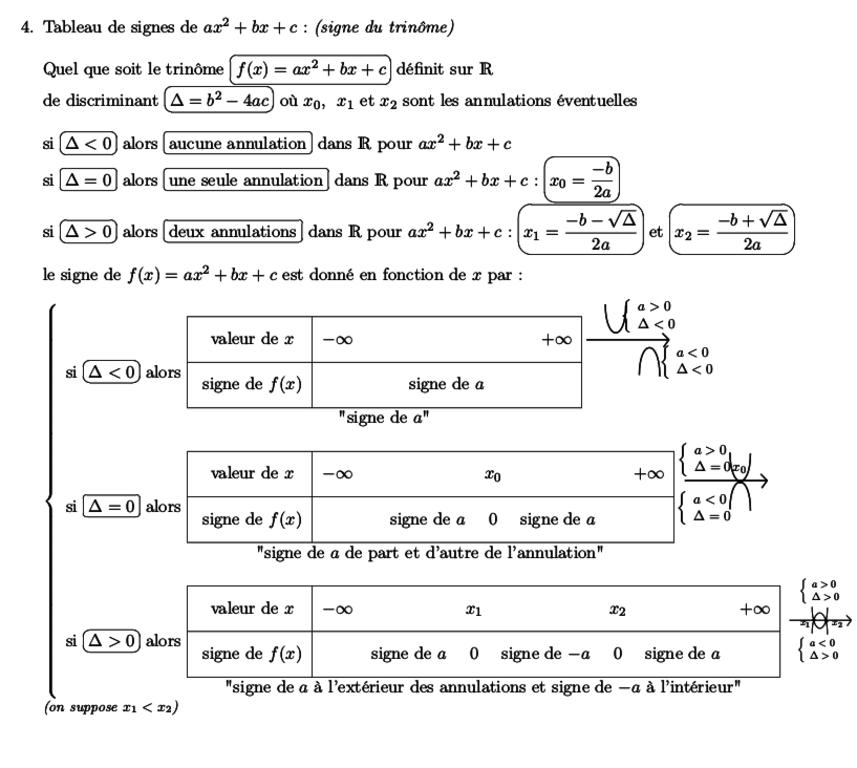
pour les exercices qui suivent, on fait une étude de signe au brouillon,
(ou on utilise la règle du signe d'un trinôme)
☺Enfin !
on peut résoudre des problèmes d'optimisation grâce à la dérivation
- tp_fonction_degre_deux_c_r_b $tp_fonction_degre_deux_c_r_b
-
Votre moyenne est pour le moment de : $moyenne_derivation_niveau_1