POURQUOI LES NOMBRES ENTIERS NATURELS : \( \mathbb N \) ?
\( \mathbb N = \{ 0, 1, 2, ...,100, 101, ... \} \)
Pour DÉNOMBRER ( COMPTER ) des objets, des choses ...
Les Nombres Entiers Naturels permettent de dire
COMBIEN il y a d'objets, de choses... "entières"
(0 chose, 1 chose, 2 choses, ...)
0
0+1 =
1
0+1+1 = 2
0+1+1+1 = 3
0+1+1+1+1 = 4
...
et ainsi de suite
...
On commence de 0 et on obtient l'entier naturel
suivant en ajoutant 1
et ainsi de suite...
On obtient par ce procédé
l'ensemble noté \( \mathbb N \),
"l'ensemble des entiers positifs ou nuls",
aussi appelé
"l'ensemble des entiers Naturels ".
Les nombres entiers naturels permettent de
préciser combien il y a d'éléments
dans l'ensemble que l'on considère,
quel que soit le nombre d'éléments de cet ensemble.
Il est "utile" de représenter les nombres entiers naturels sur une droite graduée, 0 est associé au point O, l'origine du repère, 1 est associé au point I, le point unitaire du repère.
Les entiers naturels se suivent sur cette droite orientée par convention vers la droite.
Un petit Zoom.

(pièges ?)

1 goutte + 1 goutte = 1 goutte


Dans l'histoire, il y a eu plusieurs "systèmes" pour
écrire les entiers naturels.
Os Gravés d'Ishango ( vers - 23000 ans )
Homo sapiens-sapiens -> pour le comptage ?
cet os aurait pu permettre de compter ( des jours, des objets, ... )
 (clic sur l'image vers wikipédia) |
Des Gravure sur un OS !
On fait des encoches une à une sur un os,
jusqu'à ce qu'il y en ait autant que le nombre que l'on considère.
Boule d'argiles creuse et CALCULIS
en Mésopotamie ( -3500 )
"Un caillou pour un mouton" n'est pas pratique !
on fabrique alors des "calculis" en argile :
des billes (grosses ou petites),
des grosses billes perforées,
des cônes (grands ou petits),
des grands cônes perforés.
Ces petits "calculis" d'argile sont enfermés dans une boule creuse
sur laquelle sont marqués le contenu et un sceau ("signature")
( La bulle "enveloppe" permet de sécuriser le transport de marchandise, d'animaux,...
on casse la boule pour connaître le nombre d'animaux qui ont été transportés
et vérifier qu'il n'en manque pas à l'arrivée.)
Boule d'argiles APPLATIE et ÉCRITURE des NOMBRES
en Mésopotamie ( -3400 )
Plus besoin de Petits "calculis" d'argile, on aplatit la boule creuse
et on laisse uniquement la trace que laisse le calculi sur la boule d'argile écrasée.
Plus besoin de boule d'argile.
C'est le début de l'écriture !
 |
Par exemple : ( écriture cunéiforme positionnelle )
Écriture des nombres entiers naturels
en Basse Mésopotamie entre 3400 et 3300 av. J.-C
essayez de comprendre "comment cela fonctionne" ! |
HIÉROGLYPHES et écriture des nombres
en Égypte ( -2000 )
Par exemple : ( écriture Égyptienne additionnelle)
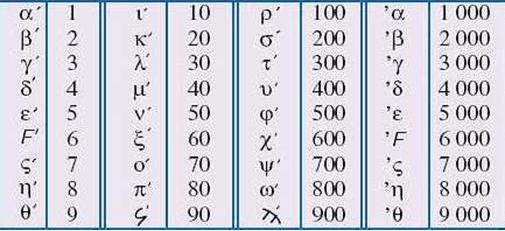
ÉCRITURE des NOMBRES ENTIERS
en Grèce ( - 700)
(comprenez comment cela fonctionne !) |
ÉCRITURE ROMAINE ( -500 )
|
DIX = 509 MM = 2000 MCMXCVIV = 1999 \(\overline{IV}DCCCLXXXVIII \) = 4 888 (là c'est un peu plus compliqué à comprendre car il y a parfois des soustractions à faire ! |
ÉCRITURE POSITIONNELLE en base 10 actuelle
avec les 10 chiffres
(0,1,2,3,4,5,6,7,8,9)
| 21408
= 2 \( \times \) 10000 +1 \( \times \) 1000 +4 \( \times \) 100 + 0 \( \times \) 10 + 8 \( \times \) 1 Là c'est plus simple ! |
Le système de numération en "base dix" permet potentiellement d'écrire tous les entiers naturels, sans exception, dans l'ordre croissant en partant de 0. Il suffit d'apprendre les dix chiffres et la méthode pour les écrire à la queue leu leu.
21408 \( 21408 = 2 \times 10^4 + 1 \times 10^3 + 4 \times 10^2 + 0 \times 10^1 + 8 \times 10^0\)on peut utiliser les puissance de dix pour éviter tous les zéros ... |
Par exemple :
( positionnelle binaire c'est à dire en base 2)
Le nombre entier naturel qui s'écrit \(11\) en base dix, Remarque : en base 2, on a : les entiers naturels sont alors notés : |
ÉCRITURE POSITIONNELLE en base 0 ≤ b ≤ 62
avec les 62 "chiffres"
(0,1,2,3,4,5,6,7,8,9, ..., z)
Exemple du nombre 164571 écrit selon
divers systèmes de numération
Conversion automatique vers
divers systèmes de numération
Le plus grand nombre que vous aurez vu écrit en base 10
POURQUOI LES NOMBRES ENTIERS RELATIFS : \( \mathbb Z \) ?
\( \mathbb Z = \{ ...,-101, -100, ..., -1, 0, 1, 2, ..., 100, 101, ...\} \)
Pour rendre compte d'une dette
où
d'un solde de compte en banque "débiteur", "à découvert" ...
Solde du compte = -2000 euros
 |
Pour rendre compte d'une Température Négative :
(plus petite que 0)
Il fait -4°C .
Pour POSITIONNER un point sur un axe :
A a pour Abscisse -2
 |
Pour POSITIONNER un point dans un repère du plan :
M(-3,-4).
 |
Pour rendre compte d'une baisse :
Évolution des prix de -10%
 |
...
0
0-1 = -1
0-1-1 = -2
0-1-1-1 = -3
0-1-1-1-1 = -4
...
et ainsi de suite
...
On commence de 0 et on obtient l'entier négatif
précédents en soustrayant 1.
(en ajoutant -1)
On obtient par ce procédé
l'ensemble noté \( \mathbb N^- \)
"l'ensemble des entiers négatifs ou nuls".
Si on considère l'ensemble des entiers
"positifs ou négatifs ou nuls"
on parle de l'ensemble des "entiers relatifs"
que l'on note : \( \mathbb Z \)
Un petit Zoom.

Comment écrire
(et calculer avec )
les entiers relatifs ?
EN CHINE ( -100 )
Couleurs différentes selon le signe
EN INDE ( 500 )
Premières règles de calcul
EN FRANCE( 1800 )
Notation actuelle avec un signe + ou -
( Règles des signes )
POURQUOI LES NOMBRES DÉCIMAUX : \( \mathbb D \) ?
( fractions décimales )
Pour les mêmes raisons xistent les fractions.
Si on veut, par exemple, mesurer la longueur d'une corde.

Il faut une unité de mesure de longueur !
C'est le "mètre étalon"
(qui fixe la longueur du mètre)

 | |||
    | |||
1 |
2 |
3 |
4 |
"cela tombe juste !"
(Autres exemples où cela tombe juste)

Et si cela ne "tombe pas juste ?"
 | |||
    | |||
1 |
2 |
3 |
4 |
Pour plus de précision, on "divise" le mètre étalon en dix parts égales (en dixièmes), chacune des parts a pour mesure \( \dfrac{1}{10}\) de mètres, que l'on peut écrire 0,1 mètres.

 | |||
    | |||
1 |
2 |
3 |
0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1
|
que l'on peut écrire 3,4 et 3,5 mètres.
Cela ne tombe toujours pas juste !
Pour plus de précision, on divise chaque dixième de mètre en dix parts égales (en centièmes de mètres), chacune des parts mesure \( \dfrac{1}{100}\) de mètres, que l'on peut écrire 0,01 mètres.

La corde mesure entre \( 3 + \dfrac{4}{10} + \dfrac{5}{100}\) et \( 3 + \dfrac{4}{10} + \dfrac{6}{100}\) mètres, que l'on peut écrire 3,45 et 3,46 mètres.
et ainsi de suite jusqu'à ce que cela "tombe juste" si cela arrive !
Zoom dynamique continu sur la droite Numérique Réelle Mesurer une longueur

Un petit Zoom qui semble ne pas finir ! .

Un petit Zoom qui semble finir ! .

les nombres décimaux permettent d' exprimer des mesures "simplement" dans le "système métrique décimal" ( déci, centi, milli,...) avec une certaine précision.
\( \pi \simeq 3,14 \)
Valeur approchée de \( \pi \) à 0,01 près.
il permettent aussi d'encadrer la mesure par deux décimaux, avec une certaine amplitude.
\( 3,1 \leq \pi \leq 3,2 \)
encadrement de \( \pi\) d'amplitude 0,1.
Les nombres décimaux "sont repèrés" par les graduations d'une règle graduée.
Un petit Zoom (in et out) |
La notation décimale très pratique comme par exemple 3,45 avec la virgule est relativement récente, ce n'est qu'en 1920 que la conférence
internationale de Strasbourg recommande l'utilisation de la virgule dans tous les textes
mathématiques.
Belgique, notation proche de celle actuelle ( 1600 )
\( 2 + \dfrac{5}{10} + \dfrac{7}{100} \) s'écrivait  en 1548
en 1548
avant de passer par
2 | 57
2;57
2| 57
25'7'
et d'autres notations durant le XVII ème siècle
pour finir par
2,57 en 1920.
On peut écrire un nombre décimal avec la notation avec la virgule, ou avec les fractions décimales, ou encore avec la notation avec les puissances de dix.
On peut dire qu'un nombre décimal est un nombre "qui peut s'écrire" avec un nombre fini de chiffres après la virgule.
("mais pas que", car par exemple : 2 = 1,99999)
L'ensemble des nombres décimaux est noté \( \mathbb{D} \)
POURQUOI LES NOMBRES RATIONNELS : \( \mathbb Q \) ?
( fractions )
il y a strictement plus de deux gâteaux et strictement moins de trois gâteaux !
Pour pouvoir rendre compte d'un partage,
du "fractionnement" d'une unité !
( 1/8 pour l'un et 7/8 pour l'autre )
Pour pouvoir rendre compte d'une mesure fractionnaire
( 3/4 d'unité, ...)
Pour pouvoir rendre compte d'une "évolution relative" écrite en %
( Le prix augmente de 15% par semaine )
 |
...
Un petit Zoom in et out.

Zoom Mesure Rationnelle

Il a existé plusieurs "systèmes" pour écrire les fractions
Tablettes et ÉCRITURE des FRACTIONS
en Mésopotamie
( -3000 )
FRACTIONS ÉGYPTIENNES
( -2000 )
Pratiquement que des fractions de numérateur 1 |
Visualisation graphique de l'écriture décimale périodique d'un rationnel

Au MOYEN ORIENT
notation des fractions avec la barre actuelle
( vers l'an 1000 )
Insuffisance des (fractions) nombres rationnels
pour décrire le monde ?
En GRÈCE, Pythagore et ses disciples montrent que
la mesure de la diagonale du carré de côté 1
n'est pas une fraction
( c'est \( \sqrt{2}\) ! )
( -500)
POURQUOI LES NOMBRES IRRATIONNELS : \( \mathbb R \setminus \mathbb Q \) ?
(-> vers les nombres irrationnels)
En GRÈCE, Pythagore et ses disciples montrent que
la mesure de la diagonale du carré de côté 1
n'est pas une fraction
( c'est \( \sqrt{2}\) ! )
( -500)
En France, Lambert montre que
pi = \( \pi \simeq 3,1415926...\)n'est pas une fraction
( 1760 )

On appelle alors tous les nombres qui ne sont
pas des Fractions
des nombres Irrationnels
POURQUOI LES NOMBRES RÉELS : \( \mathbb R \) ?
Une fois que l'on a jouté aux fractions (positives et négatives),
l'ensemble des nombres Irrationnels
on obtient l'ensemble noté \( \mathbb R \) ,
l'ensemble des nombres Réels.
\( \mathbb R \) modélise l'ensemble des abscisses de tous les points d'une droite
à chaque point correspond un seul nombre
et réciproquement
Un petit Zoom in et out.
Pour pouvoir associer une mesure à toute grandeur
( à toute longueur, aire, masse, durée , ...)
 |
POURQUOI LES NOMBRES COMPLEXES : \( \mathbb C \) ?
\( x^2 = -1 \) pour \( x = ? \)
( fin de l'histoire pour les secondes,
mais l'histoire continue ...
)
On résume (très) Grossièrement de \( \mathbb N \) à \( \mathbb R \) ?
| \( \mathbb N \) : -> pour compter les Mammouths (j'ai vu 3 Mammouths !) |
| \( \mathbb Z \) : -> pour distinguer le positif du négatif (s'orienter) (Il fait -3 degrés !) |
| \( \mathbb Q \) : -> pour partager (l'héritage , ...) (J'ai eu 1/3 de la tarte) |
| \( \mathbb D \) : -> pour utiliser le système métrique, pour mesurer, c'est plus pratique ! (Je mesure 1,65 mètres) |
| \( \mathbb R \) : -> pour pouvoir mesurer n'importe quelle longueur, masse, ... (La diagonale d'un carrée de coté 1 mètre, mesure \(\sqrt{2}\) mètres), (Le périmètre d'une roue de 1 mètre de diamètre mesure \( \pi\) mètres) |
Méthode : CQQCOQP |
| C : Comment -> en cherchant à résoudre des problèmes |
| Q : Qui -> les Humains |
| Q : Quand-> tout au long de l'histoire |
| C : Combien -> beaucoup |
| O : Où -> partout sur terre |
| Q : Quoi -> inventer les nombres ci-dessus |
| P : Pourquoi -> pour dénombrer, mesurer ... |