Cours : Multiple et Division Euclidienne pour les entiers naturels
Introduction
Ce qui suit est un rappel sur la division Euclidienne, celle-ci sera (très) utile par la suite.
La propriété qui suit sera utilisée pour montrer qu'un entier naturel est ou n'est pas un multiple d'un autre entier naturel
Voici une petite "visualisation" sur la division euclidienne (ceci)
Attention : Propriété (Rappel sur la division Euclidienne pour les entiers naturels)
Quels que soient les entiers naturels \(a\) et \(b \neq 0\)
Il existe deux uniques nombres entiers naturels \(q\) et \(r\) tels que : \(\displaystyle \left\{ \begin{array}{l} a=bq+r \\ et \\ 0 \leq r < b \end{array} \right.\)
La division Euclidienne de \(a\) par \(b\) s'écrit : \(a=bq+r\)
\(a\) est appelé le "dividende",
\(b\) est le "diviseur",
\(q\) est le "quotient"
\(r\) est "le reste".
Exemple : On cherche la division Euclidienne de 371 par 17
À la calculatrice : \(\dfrac{371}{ 17} \simeq 21,8235...\)
On arrondi "à l'entier inférieur ou égal" pour obtenir le quotient \(q = 21\)
Donc on a : \(371 = 17 \times 21 + r\)
Puis, pour obtenir le reste, on fait le calcul : \(r = 371 - 17 \times 21 = 14\)
On vérifie \(371 = 17 \times 21 + 14\)
Conclusion :
la division Euclidienne de \(371\) par \(17\) donne \(371 = 17 \times 21 + 14\) avec \(q = 21\) et \(r = 14\)
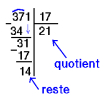
À la main avec papier crayon
On pose la division comme on a appris à le faire il y a quelques temps
et on obtient : \(371 = 17 \times 21 + 14\)
Remarque :
Le reste de la division Euclidienne de a par b est donné directement par certaines calculatrice.
il suffit ( comme dans le langage de programmation Python) d'entrer a%b pour obtenir directement le reste
par exemple : 7%2 = 1 signifie que le reste de la division Euclidienne de 7 par 2 est égal à 1
Essayez de la faire avec votre calculatrice
À partir de la définition de "multiple", il est possible de reformuler la notion de multiple, ce qui donnera une méthode efficace pour démontrer qu'un nombre entier naturel n'est pas ou est un multiple d'un autre en utilisant la division Euclidienne.
Attention : Propriété (multiple et division Euclidienne pour les entiers naturels) (admise)
Quels que soient les nombres entiers naturels \(a\) et \(b \neq 0\).
\(a\) est un multiple de \(b\)
équivaut à
le reste de la division Euclidienne de \(a\) par \(b\) est égal à \(0\)
Complément : Logique : Démonstration d'une équivalence par la méthode de la "double implication"
Principe de la démonstration d'une équivalence par la méthode de la "double implication"
Quand on veut démontrer une proposition de la forme :
"condition 1" équivaut à "condition 2"
on démontre l'implication directe : "Si condition 1 Alors Condition 2"
on démontre l'implication réciproque : "Si condition 2 Alors Condition 2"
Application pour la propriété précédente :
Démontrons :
Quels que soient les nombres entiers naturels \(a\) et \(b \neq 0\).
\(a\) est un multiple de \(b\)
équivaut à
le reste de la division Euclidienne de \(a\) par \(b\) est égal à \(0\)
Exemple :
Montrons que \(29\) n'est pas un multiple de \(3\) en utilisant la propriété ci-dessus.
Il suffit de faire la division Euclidienne de \(29\) par \(3\)
Ce qui donne :\( 29=3 \times 9+2\)
On constate que le reste de la division Euclidienne de \(29\) par \(3\) est \(2\) qui est non nul.
Conclusion : \(29\) n'est pas un multiple de \(3\)
Montrons que \(27\) est un multiple de \(3\) en utilisant la propriété ci-dessus.
La division Euclidienne de \(27\) par \(3\) donne : \(27=3 \times 9+0\)
On constate que le reste de la division Euclidienne de \(27\) par \(3\) est \(0\)
Conclusion : \(27\) est un multiple de \(3\)
Remarque :
Pour justifier qu'un entier naturel \(a\), est, ou n'est pas, un multiple d'un entier naturel \(b\) non nul, Il suffit d'effectuer la division euclidienne de \(a\) par \(b\) et de constater si le reste est nul ou pas. Cela constitue un moyen "algorithmique" de donner une justification
Pour les entiers relatifs négatifs, on considère les valeurs absolues des entiers et on applique la méthode précédente, puis on utilise le fait que :
Pour tout entier \(a\), \(a\) est un multiple de \(b\) si et seulement si \(a\) est un multiple de \(-b\)
Pour tout entier \(a\), \(a\) est un multiple de \(b\) si et seulement si \(-a\) est un multiple de \(b\)
\(27\) est un multiple de \(3\)
\(27\) est un multiple de \(-3\)
\(-27\) est un multiple de \(3\)
\(-27\) est un multiple de \(-3\)