Cours : Multiple
Texte légal :
Considérons dans un premier temps l'ensemble des nombres entiers naturels (voir),
cherchons s'il existe des liens entre les entiers naturels (voir),
peut-on obtenir certains à partir de certains autres ? (par les opérations de base et plus particulièrement la multiplication ou la division) ?
Peut-on obtenir certains entiers naturels à partir d'un entier naturel plus petit par multiplications ?
Donner des exemples.
Comment appelle t-on alors le plus grand par rapport au plus petit ?
Comment appelle t-on alors le plus petit par rapport au plus grand ?
Existe t-il des entiers naturels qui ne peuvent pas être construits par multiplication d'entiers plus petits ?
Donner des exemples ?
Comment appelle t-on de tels nombre entiers ?
Comment sont "fabriqués" les "multiples" d'un nombre entier quelconque (naturel ou relatif) ?
Partons de 0 et ajoutons 0 autant de fois que l'on veut, on obtient toujours 0 !
On dit que L'ensemble des "multiples de 0" est : {0}
Partons de 0 et ajoutons ou soustrayons 1 autant de fois que l'on veut, on obtient l'ensemble : {... ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; ...}.
L'ensemble des "multiples de 1 " est l'ensemble des entiers Relatifs
Partons de 0 et ajoutons ou soustrayons 2 autant de fois que l'on veut, on obtient l'ensemble : {... ; -6 ; -4 ; -2 ; 0 ; 2 ; 4 ; 6 ; ...}
L'ensemble des "multiples de 2" est l'ensemble des nombres pairs.
Pour 3 : on obtient l'ensemble {... ; -6 ; -3 ; 0 ; 3 ; 6 ; ...}
Pour \(a \in Z\) : on obtient { ... ; -4a ; -3a ; -2a ; -a ; 0 ; a ; 2a ; 3a ; 4a ; ... }
encore noté \(\{a \times k ~|~ k \in \mathbb Z \}\)~~~~~( "|" se lit "tel que" )
Pour voir l'ensemble des multiples positifs d'un entier positif (donc naturel) (ceci)
Définition :
Définition (Multiple) :
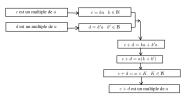
Quels que soient les nombres entiers relatifs \(a \in \mathbb Z\) et \(b \in \mathbb Z\)
\(a\) est un multiple de \(b\)
équivaut à
Il existe un entier relatif \(k \in Z\) tel que \(a = bk\)
Exemple :
\(6 = 2 \times 3\) et \(3 \in \mathbb Z\)
donc Il existe un entier relatif \(k \in Z\) tel que \(6 = 2k\)
donc \(6\) est un multiple de \(2\)
\(-21 = 3 \times (-7)\) et \(-7 \in \mathbb Z\)
donc Il existe un entier relatif \(k \in Z\) tel que \(-21 = 3k\)
donc \(-21\) est un multiple de \(3\)
Exemple : contre-exemple
3 n'est pas un multiple de 0
(la justification est détaillée ci-dessous en complément pour mettre en évidence la méthode du "raisonnement par l'absurde)
3 n'est pas un multiple de 2
(justification aussi détaillée ci-dessous)
Complément : Logique : Démonstration par la méthode du "Raisonnement par l'absurde"
Méthode du Raisonnement par l'absurde :
Principe du raisonnement par l'absurde.
Pour démontrer une "proposition"
on suppose la négation de cette proposition
on fait des déductions logiques jusqu'à ce que l'on arrive à une "absurdité" (une contradiction)
on conclut la proposition initiale est valide
Utilisation du raisonnement par l'absurde.
Démontrons la proposition : "\(3\) n'est pas un multiple de \(0\)"
Supposons la négation de cette proposition
c'est à dire, supposons que : \(3\) est un multiple de \(0\)
alors : Il existe un entier relatif \(k \in \mathbb Z\) tel que \(3 = k \times 0\) (définition ci-dessus)
alors : \(3 = 0\)
ce qui est absurde ! ( car \(3\neq 0)\)
donc : \(3\) n'est pas un multiple de \(0\)
\(~~\)
Démontrons la proposition : "\(3\) n'est pas un multiple de \(2\)"
Supposons la négation de cette proposition
c'est à dire, supposons que : \(3\) est un multiple de \(2\)
alors : Il existe un entier relatif \(k \in \mathbb Z\) tel que \(3 = k \times 0\) (définition ci-dessus)
alors : \(3 = 2k_0\) et \(k_0 \in \mathbb Z\)
or : \(2 < 3 < 4\)
alors : \(2 < 2k_0 < 4\)
alors : \(1 < k_0 < 2\)
ce qui est absurde car il n'existe pas d'entier relatif strictement compris entre \(1\) et \(2\)
donc : \(3\) n'est pas un multiple de \(2\)
\(~\)
On peut procéder ainsi pour démontrer qu'un certain entier relatif n'est pas un multiple d'un autre mais il y a une méthode plus "rapide" avec la "division euclidienne" ou avec la division des réels.
Ce qui est vu par la suite
Remarque : (admis)
La définition ci-dessus ne dit pas comment on obtient \(k\) à partir de \(a\) et \(b\), elle dit qu'il existe (au moins) une valeur de \(k\).
Une méthode pour trouver \(k\) (si \(k\) existe) est donnée par la suite
Pour montrer qu'un entier relatif \(a\) est un multiple d'un entier relatif \(b\),
il suffit de réussir à prouver que : \(a = bk\) et \(k \in \mathbb Z\)
Pour montrer qu'un entier relatif \(a\) n'est pas un multiple d'un entier relatif \(b\),
on peut raisonner par l'absurde comme dans l'exemple ci-dessus (pour \(3\) et \(2\)),
une autre méthode utilisant la division Euclidienne est donnée par la suite.
\(0\) n'admet qu'un seul multiple, \(0\) lui même
Tout nombre entier \(n\) est un multiple de lui même
Tout nombre entier non nul admet une infinité de multiples
\(-1\) et \(1\) ont \(\mathbb Z\) pour ensemble de multiples
L'ensemble des multiples de \(2\) est appelé l'ensemble des entiers "pairs"
Il existe des entiers relatifs \(a\) et \(b\) tels que \(a\) est multiple de \(b\) et \(b\) est multiple de \(a\) (en même temps)
\(-3\) est un multiple de \(3\) et \(3\) est un multiple de \(-3\)
Pour tout entier \(a\), \(a\) est un multiple de \(b\) si et seulement si \(a\) est un multiple de \(-b\)
Pour tout entier \(a\), \(a\) est un multiple de \(b\) si et seulement si \(-a\) est un multiple de \(b\)
Tout nombre entier non nul \(n\) admet un multiple qui lui est strictement inférieur
\(-1\) est un multiple de \(1\) et \(-1 < 1\)
Pour les entiers naturels uniquement :
Quels que soient les entiers naturels \(a\) et \(b\),
\(a\) est multiple de \(b\) et \(b\) est multiple de \(a\)
si et seulement si \(a = b\)
Pour les entiers naturels uniquement :
Quels que soient les entiers naturels \(a\) et \(b\),
Si \(a\) est un multiple de \(b\) et \(a\) est positif strict
Alors \(a \geq b\)
Complément : Logique : (négation d'une proposition de la forme "il existe x P(x)" ) (cliquer)
Négation d'une proposition de la forme : Il existe \(x\), \(P(x)\)
La négation d'une proposition de la forme : \(\exists x,P(x)\)
où \(\exists\) se lit "il existe" et \(P(x)\) est un "prédicat de la variable \(x\)"
est :
\(\forall x ~ non P(x)\)
où :
_\(\forall \)se lit "quel que soit"
_ "non \(P(x)\) est la "négation" de \(P(x)\)
\(~\)
on a donc, par exemple :
La "négation de la proposition :
"Il existe un entier relatif \(k \in \mathbb Z\) tel que \(a = k \times b\)"
est
"Il n'existe pas d'entier relatif \(k \in \mathbb Z\) tel que \(a = k \times b\)"
qui peut encore s'écrire :
"Quel que soit l'entier relatif \(k \in \mathbb Z\), \(a \neq k \times b\)"
Ce qui conduit à dire que :
Quels que soient les nombres entiers relatifs \(a \in \mathbb Z\) et \(b \in Z\)
\(a\) n'est pas un multiple de \(b\)
signifie que
"Quel que soit l'entier relatif \(k \in \mathbb Z\), \(a \neq k \times b\)"
Complément : (autre démonstration) (cliquer)
Autre Démonstration :
Démontrer que la proposition : "\(3\) n'est pas un multiple de \(0\)"
Revient à démontrer que : "Quel que soit l'entier relatif \(k \in \mathbb Z \), \(3 \neq k \times 0\)"
Soit \(k_0 \in \mathbb Z\) un entier relatif quelconque
on a : \(k_0 \times 0 = 0\)
or : \(3 \neq 0\)
donc : \(3 \neq k_0 \times 0\)
donc : "Quel que soit l'entier relatif \(k \in \mathbb Z\), \(3 \neq k \times 0\)"
Conclusion : "\(3\) n'est pas un multiple de \(0\)"
Attention : Propriété exemplaire
Propriété exemplaire ( multiple et somme )
Quels que soient les nombres entiers relatifs \(a,c\) et \(d\)
Si \(c\) et \(d\) sont des multiples de \(a\)
Alors \(c+d\) est un multiple de \(a\)
Complément : Méthode de démonstration par "implications successives"
Démontrons la propriété ci-dessus par la méthode des "implications successives"
Principe du raisonnement par implications successives quand on souhaite démontrer qu'une proposition de la forme "Si condition Alors conclusion" est vraie.
On prend la condition pour hypothèse
On fait une succession de déductions
On arrive à la conclusion
Application pour la démonstration de la propriété ci-dessus
Soient \(a,b\) et c trois entiers relatifs quelconques
Supposons que \(c\) et \(d\) soient des multiples de \(a\)
\(c\) est un multiple de \(a\)
soit alors \(k \in \mathbb Z\) tel que \(c = ka\)
\(d\) est un multiple de \(a\)
soit alors \(k' \in Z\) tel que \(d = k'a\)
\(c + d = ka+k'a = a(k+k') = aK\) en posant \(K = k+k'\) avec \(K \in Z\)
alors il existe un entier \(K\) tel que \(c+d=Ka\)
Donc \(c+d\) est un multiple de \(a\)
Quels que soient les nombres entiers relatifs \(a,c\) et \(d\)
Si \(c\) et \(d\) sont des multiples de \(a\)
Alors \(c+d\) est un multiple de \(a\)
Exemple :
Si on additionne un multiple quelconque de \(2\) avec un multiple quelconque de \(2\) alors on obtient un multiple de \(2\)
Si on additionne un multiple quelconque de \(-5\) avec un multiple quelconque de \(-5\) alors on obtient un multiple de \(-5\)
Remarque :
Un multiple quelconque de \(2\) plus un multiple quelconque de \(3\) donne ?
(surtout pas un multiple de de 5 !)
Il y a "plein" de questions "de ce genre" que l'on peut se poser et chercher à justifier.